$\newcommand{\dede}[2]{\frac{\partial #1}{\partial #2} } \newcommand{\dd}[2]{\frac{\mathrm{d} #1}{\mathrm{d} #2}} \newcommand{\divby}[1]{\frac{1}{#1} } \newcommand{\typing}[3][\Gamma]{#1 \vdash #2 : #3} \newcommand{\xyz}[0]{(x,y,z)} \newcommand{\xyzt}[0]{(x,y,z,t)} \newcommand{\hams}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyz} \newcommand{\hamt}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2} + \dede{^2}{y^2} + \dede{^2}{z^2}) + V\xyzt} \newcommand{\ham}[0]{-\frac{\hbar^2}{2m}(\dede{^2}{x^2}) + V(x)} \newcommand{\abs}[1]{\left|\left| #1 \right|\right|} \newcommand{\unit}[1]{\, \mathrm{#1}}$
Woche 1 - Einführung
Beispiele wie die Übungen gelöst werden sollten
Aufgabe 1
Daniel wirft einen Ball der Masse $m$ unter einem Winkel $\alpha=45^\circ$ zum Boden nach links. Mit welcher Anfangsgeschwindigkeit $v_0$ muss er den Ball werfen, damit dieser eine Distanz von $d=10\,\mathrm{m}$ zurücklegt? Der Luftwiderstand sei dabei vernachlässigbar und es darf angenommen werden, dass der Ball auf der gleichen Höhe wie der Abwurfpunkt landet.
Lösung 1
-
Wir fertigen eine Skizze an:

-
Physikalische Bedingungen:
Da wir den Luftwiderstand vernachlässigen können, wirkt auf den Ball lediglich die Gravitationskraft. Damit gilt für die Bewegungsgleichungen:
-
Bewegungsgleichungen:
$$\ddot{x} = 0 \qquad (1x) $$ $$\ddot{y} = -g \qquad (1y) $$
-
Lösen der Gleichungen:
Zweifaches integrieren von (1x) liefert:
$$x(t) = v_{0,x} t + x_0 \qquad (2x)$$
Zweifaches integrieren von (1y) liefert:
$$y(t) = -\frac{1}{2} g t^2 + v_{0,y} t + y_0 \qquad (2y)$$
Da der Ball auf der gleichen Höhe wie der Abwurfpunkt landet, gilt $y_0 = 0$ und $x_0$ kann weggelassen werden, der Abstand der Landeposition zur Startposition gesucht wird. Ausserdem gilt $v_{0,x} = v_0 \cos(\alpha)$ und $v_{0,y} = v_0 \sin(\alpha).$ Nun setzen wir $t_{end}$ als den Zeitpunkt, bei dem der Ball landet und erhalten:
$$x(t_{end}) = d \qquad (3x)$$ $$y(t_{end}) = 0 \qquad (3y)$$
Einsetzen von (2x) und (2y) in (3x) und (3y) liefert:
$$v_0 \cos(\alpha) t_{end} = d \qquad (4x)$$ $$-\frac{1}{2} g t_{end}^2 + v_0 \sin(\alpha) t_{end} = 0 \qquad (4y)$$
Auflösen von (4x) nach $t_{end}$ liefert:
$$t_{end} = \frac{d}{v_0 \cos(\alpha)} \qquad (5)$$
Einsetzen von (5) in (4y) liefert:
$$-\frac{1}{2} g \left(\frac{d}{v_0 \cos(\alpha)}\right)^2 + v_0 \sin(\alpha) \frac{d}{v_0 \cos(\alpha)} = 0 \qquad (6)$$
Auflösen von (6) nach $v_0$ liefert:
$$\abs{v_0} = \sqrt{\frac{g d}{2 \sin(\alpha) \cos(\alpha)}}$$
-
Ausrechnen des numerischen Resultates:
Einsetzen der Werte $g=9.81\,\mathrm{m/s^2}$, $d=10\,\mathrm{m}$ und $\alpha=45^\circ$ liefert:
$$\abs{v_0} = \sqrt{\frac{9.81\,\mathrm{m/s^2} \cdot 10\,\mathrm{m}}{2 \cdot \sin(45^\circ) \cdot \cos(45^\circ)}} \approx 9.9 \,\mathrm{m/s}$$
-
Sanity check:
Die Einheit $\mathrm{m/s}$ entspricht einer Geschwindigkeit, wie gewünscht. Der Betrag entspricht etwa einer Geschwindigkeit von $36\,\mathrm{km/h}$, was für einen Ballwurf, der $10\, \mathrm{m}$ weit kommt realistisch ist.
Aufgabe 2 - Dient nur der Demonstration!
Falls du mir nach der im Unterricht gezeigten Aufgabe 1 nicht glaubst, dass es sich lohnt diesem Schema zu folgen, habe ich hier noch eine etwas schwierigere gemacht. Diese ist aber in keinster Weise prüfungsrelevant und dient nur zur Demonstration des Lösungsschemas.
Ein Fallschirmspringer springt aus grosser Höhe aus einem Flugzeug. Die Anfangsgeschwindigkeit beträgt $v_0=0\,\mathrm{m/s}$ und die Anfangshöhe $h_0=2000\,\mathrm{m}.$ Die Masse des Fallschirmspringers beträgt $m=100\,\mathrm{kg}.$ Die Gravitationskraft beträgt $g=9.81\,\mathrm{m/s^2}$ und kann als konstant angenommen werden. Welche Geschwindigkeit erreicht der Fallschirmspringer, falls er den Fallschirm nicht öffnet wenn er am Boden aufschlägt? Der Luftwiderstand beträgt $F_W = -\frac{1}{2} \rho C_W A v^2$ mit $\rho(h)=1.2\,\mathrm{kg/m^3} * 2^{-h/(5500\, \mathrm{m})}$ der Dichte der Luft, $C_W=1.4$ dem spezifischen Koeffizienten und $A=1\,\mathrm{m^2}$ der Angriffsfläche.
Lösung 2
-
Wir fertigen eine Skizze an:
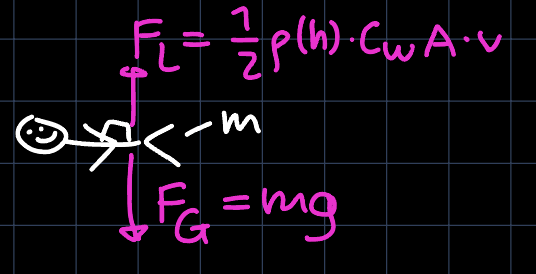
-
Physikalische Bedingungen:
Da wir den Luftwiderstand berücksichtigen, wirkt auf den Fallschirmspringer die Gravitationskraft und der Luftwiderstand. Da die Anfangsgeschwindigkeit $v_0=0\,\mathrm{m/s}$ beträgt, wirkt die Gravitationskraft immer in Bewegungsrichtung und der Luftwiderstand immer entgegen der Bewegungsrichtung. Also ergibt sich die effektive Kraft aus der Differenz der beiden Kräfte:
-
Bewegungsgleichung:
$$F_{eff} = F_G + F_W = m \ddot{y} \qquad (1)$$
$$F_G = m g \qquad (2)$$
$$F_W(y) = -\frac{1}{2} \rho(y) C_W A \dot{y}^2 \qquad (3)$$
-
Lösen der Bewegungsgleichung:
Einsetzen von (2) und (3) in (1) liefert:
$$m g -\frac{1}{2} \rho(y) C_W A \dot{y}^2 = m \ddot{y} \qquad (4)$$
Auflösen von (4) nach $\ddot{y}$ liefert:
$$\ddot{y} = g - \frac{1}{2 m} \rho(y) C_W A \dot{y}^2 \qquad (5)$$
Es handelt sich hier um eine inhomogene Differentialgleichung zweiter Ordnung. Diese ist zu schwierig um sie analytisch zu lösen. Hier stehen also zwei Möglichkeiten zur Verfügung:
- Numerische Lösung mit einem Computerprogramm
- Vereinfachungen durch begründete Annahmen, sodass sie analytisch gelöst werden kann
Wir wählen hier die zweite Möglichkeit. Wir vereinfachen die Differentialgleichung, indem wir annehmen, dass die Dichte der Luft konstant auf dem Wert bei mittlerer Höhe von $\rho(h) \approx \rho_{avg} = 1.06\,\mathrm{kg/m^3}$ liegt. Diese Annahme ist gut begründet, da die Dichte exponentiell mit der Höhe abnimmt und keine grossen Höhen erreicht werden.
Einsetzen von $\rho(y) = \rho_{avg}$ in (5) liefert:
$$\ddot{y} = g - \frac{1}{2 m} \rho_{avg} C_W A \dot{y}^2 \qquad (6)$$
Da wir nun die Variable $y$ verloren haben, können wir eine Substitution machen. Wir definieren $v = \dot{y}$ und erhalten aus (6):
$$\dot{v} = g - \frac{1}{2 m} \rho_{avg} C_W A v^2 \qquad (7)$$
Teilen beider Seiten von (7) durch $g - \frac{1}{2 m} \rho_{avg} C_W A v^2$ und integrieren nach nach dem Separationsansatz liefert:
$$\int_{0}^{v(t)} \frac{1}{g - \frac{1}{2 m} \rho_{avg} C_W A v^2} \mathrm{d}v = \int_{0}^{t} 1 \mathrm{d}t' \qquad (8)$$
Die rechte Seite von (8) ist einfach und liefert:
$$\int_{0}^{t} 1 \mathrm{d}t' = t \qquad (9)$$
Auf der linken Seite erkennen wir, dass wir durch die Substitution $u = \sqrt{\frac{A C_W \rho_{avg}}{2 m g}} v$ und $\mathrm{d}u = \sqrt{\frac{A C_W \rho_{avg}}{2 m g}} \mathrm{d}v$ vereinfachen können:
$$\int \frac{1}{g - \frac{1}{2 m} \rho_{avg} C_W A v^2} \mathrm{d}v = \int \sqrt{\frac{2 m g}{A C_W \rho_{avg}}} \frac{1}{g - g u^2} \mathrm{d}u = \sqrt{\frac{2 m}{A C_W \rho_{avg} g}} \int \frac{1}{1-u^2} \mathrm{d}u \qquad (10)$$
Womit wir ein Integral erhalten, welches sich durch Partialbruchzerlegung lösen lässt:
$$\int \frac{1}{1-u^2} \mathrm{d}u = \int \frac{1}{1-u} \frac{1}{1+u} \mathrm{d}u = \int \left(\frac{1}{2(1+u)} - \frac{1}{2(1-u)}\right) \mathrm{d}u \qquad (11)$$
Durch das bekannte Integral $\int \frac{1}{x} \mathrm{d}x = \ln(x) + C$ und die Logarithmus-Regel $\ln(a)-\ln(b) = \ln(a/b)$ erhalten wir:
$$\int \frac{1}{1-u^2} \mathrm{d}u = \frac{1}{2} \ln \left| \frac{1+u}{1-u} \right| + C \qquad (12)$$
Durch Rücksubstitution und einsetzen von (12) in (10) erhalten wir die Stammfunktion:
$$\int \frac{1}{g - \frac{1}{2 m} \rho_{avg} C_W A v^2} \mathrm{d}v = \sqrt{\frac{2 m}{A C_W \rho_{avg} g}} \frac{1}{2} \ln \left| \frac{1+\sqrt{\frac{A C_W \rho_{avg}}{2 m g}} v}{1-\sqrt{\frac{A C_W \rho_{avg}}{2 m g}} v} \right| + C \qquad (13)$$
Damit der Ausdruck kompakt bleibt, führen wir neue Konstanten ein: $A_0 = \sqrt{\frac{2 m}{A C_W \rho_{avg} g}}$ und $B_0 = \sqrt{\frac{A C_W \rho_{avg}}{2 m g}}.$ Damit können wir die Lösung schreiben als:
$$\int \frac{1}{g - \frac{1}{2 m} \rho_{avg} C_W A v^2} \mathrm{d}v = A_0 \frac{1}{2} \ln \left| \frac{1+B_0 v}{1-B_0 v} \right| + C \qquad (13')$$
Die Bedingung (8) mit der Anfangsbedingung $v_0 = 0$ und $\ln(1) = 0$ und dem Resultat aus (9) liefert mit (13'):
$$t = A_0 \frac{1}{2} \ln \left| \frac{1+B_0 v}{1-B_0 v} \right| \qquad (14)$$
Auflösen von (14) nach $v(t)$ liefert:
$$v(t) = \frac{1}{B_0} \frac{e^{\frac{2}{A_0} t} - 1}{e^{\frac{2}{A_0} t} + 1} \qquad (15)$$
Nun können wir eine weitere Substitution der Variablennamen machen und dabei bereits etwas interpretation reinbringen: $v_{\infty} = \lim_{t \to \infty} v(t) = \frac{1}{B_0}$ ist die Geschwindigkeit, die der Fallschirmspringer erreichen würde, wenn er unendlich lange fallen würde. Weiter ist $\tau = \frac{A_0}{2}$ die Zeitkonstante, die angibt, wie schnell die Geschwindigkeit gegen $v_{\infty}$ konvergiert. Damit können wir (15) schreiben als:
$$v(t) = v_{\infty} \frac{e^{\frac{t}{\tau}} - 1}{e^{\frac{t}{\tau}} + 1} \qquad (16)$$
Nun können wir jedoch nicht einfach annehmen, dass die maximale Geschwindigkeit erreicht wird, sondern müssen zuerst die Fallzeit bestimmen. Dies können wir durch Integration der Geschwindigkeit und gleichsetzen mit der Fallhöhe $h_0$ erreichen:
$$\int_{0}^{t_{end}} v(t') \mathrm{d}t' = h_0 \qquad (17)$$
Einsetzen von (16) in (17) liefert:
$$v_{\infty} \int_{0}^{t_{end}} \frac{e^{\frac{t'}{\tau}} - 1}{e^{\frac{t'}{\tau}} + 1} \mathrm{d}t' = h_0 \qquad (18)$$
Durch die Substitution $u = e^{\frac{t'}{\tau}}$ und $\mathrm{d}u = \frac{1}{\tau} e^{\frac{t'}{\tau}} \mathrm{d}t'$ erhalten wir:
$$v_{\infty} \int_{1}^{e^{\frac{t_{end}}{\tau}}} \frac{u - 1}{u + 1} \frac{\tau}{u} \mathrm{d}u = h_0 \qquad (19)$$
Durch die Partialbruchzerlegung $\frac{u - 1}{u + 1} = 1 - \frac{2}{u + 1}$ und $\int \frac{1}{u} \mathrm{d}u = \ln(u) + C$ erhalten wir:
$$v_{\infty} \left( \tau \left( \ln(u) - 2 \ln(u + 1) \right) \right) \bigg|_{1}^{e^{\frac{t_{end}}{\tau}}} = h_0 \qquad (20)$$
Einsetzen der Randwerte ergibt:
$$v_{\infty} \left( \tau \left( \ln(e^{\frac{t_{end}}{\tau}}) - 2 \ln(e^{\frac{t_{end}}{\tau}} + 1) - \ln(1) + 2 \ln(1 + 1) \right) \right) = h_0 \qquad (21)$$
Was wir nach $t_{end}$ auflösen können:
$$t_{end} = \tau \ln \left( \frac{h_0}{v_{\infty} \tau} + 1 \right) \qquad (22)$$
Einsetzen von (22) in (16) liefert:
$$v(t_{end}) = v_{\infty} \frac{e^{\frac{t_{end}}{\tau}} - 1}{e^{\frac{t_{end}}{\tau}} + 1} = v_{\infty} \frac{\frac{h_0}{v_{\infty} \tau} + 1 - 1}{\frac{h_0}{v_{\infty} \tau} + 1 + 1} = v_{\infty} \frac{\frac{h_0}{v_{\infty} \tau}}{\frac{h_0}{v_{\infty} \tau} + 2} = v_{\infty} \frac{h_0}{h_0 + 2 v_{\infty} \tau} \qquad (23)$$
-
Ausrechnen des numerischen Resultates:
Setzten wir die gegebenen Werte $\rho_{avg} \approx 1.06\, \mathrm{kg/m^3}$, $h_0 = 2000\, \mathrm{m}$, $g = 9.81\, \mathrm{m/s^2}$, $A = 1\, \mathrm{m^2}$, $C_W = 1.4$ und $m = 100\, \mathrm{kg}$ ein, so erhalten wir:
$$v(t_{end}) \approx 34\, \mathrm{m/s} \approx 123\, \mathrm{km/h}$$
-
Logische Interpretation des Resultates:
Wir erkennen, dass die Einheiten des Resultates wie erwartet zu einer Geschwindigkeit passen. Auch der numerische Wert ist sinnvoll, da er in der Grössenordnung der Geschwindigkeit eines Falles mit Luftwiderstand liegt.
Note: Macht euch keine Sorgen, die Aufgabe war klar über dem Niveau, das im ersten Jahr erwartet wird. Sie war nur dazu da, um zu zeigen, dass einigermassen realistisch formulierte Probleme sehr schnell kompliziert werden können und daher ein strukturierter Lösungsweg wichtig ist. Sonst geht die Übersicht schnell verloren und es dauert viel länger die Aufgabe zu lösen.
Woche 2 - Kräftegleichgewichte - El und Mag
Recap Vorlesung
Nomenklatur Atomkerne
Wir haben gelernt, dass Atome doch nicht 'atomar' sind, sondern aus weiteren Elementarteilchen aufgebaut sind: Protonen, Elektronen und Neutronen. Das Periodensystem gibt uns für jedes Element eine Ordnungszahl $Z$ (Nummer oben links), die gerade der Anzahl Protonen im Atomkern entspricht. Jedoch kann ein Element eine Unterschiedliche Anzahl an Neutronen aufweisen. Deswegen wird ein Atomkern erst mit der Massenzahl $A$, die sich aus der Summe der Anzahl Protonen und Anzahl Neutronen ergibt eindeutig beschrieben. Die Bezeichnung lautet dann $_Z^A X$, wobei $X$ das Symbol des Atoms bezeichnet. Beispiele sind: $_8^{16} \mathrm{O}, _7^{14} \mathrm{N}, _6^{12} \mathrm{c}, _6^{13} \mathrm{C}.$
'Neue Einheiten'
Um nicht mit super kleinen Zahlen rechnen zu müssen, definieren wir neue Einheiten:
- Atomare Masseneinheit: $1\, \mathrm{u} = \frac{1}{12} m_{^{12}_6 \mathrm{C}}$, _amu im TR
- Elektronenvolt: $1\, \mathrm{eV} = |q_e| 1\, \mathrm{V}$ entspricht der benötigten Energie um ein Elektron durch $1\, \mathrm{V}$ zu beschleunigen.
Beispiele von Aufgaben
Schwebendes Wasser
Wir betrachten einen kugelförmigen Wassertropfen mit einem Radius von $5.0\, \mathrm{mm}$ und einer Ladung von $10\, \mathrm{\mu C}.$ Berechne das elektrische Feld, welches benötigt wird, damit der Tropfen in der Erdatmosphäre schwebt. Die Dichte von Wasser betrage $1000\, \mathrm{kg/m^3}.$
Beschleunigung im Plattenkondensator
Bestimme die kinetische Energie eines Natrium-Ions, welches in einem Plattenkondensator mit einer Spannung von $100\, \mathrm{V}$ über eine Strecke von $5\, \mathrm{cm}$ beschleunigt wird. Das elektrische Feld im Plattenkondensator ist konstant und beträgt $E = \frac{U}{d}.$
Massenspektrometer
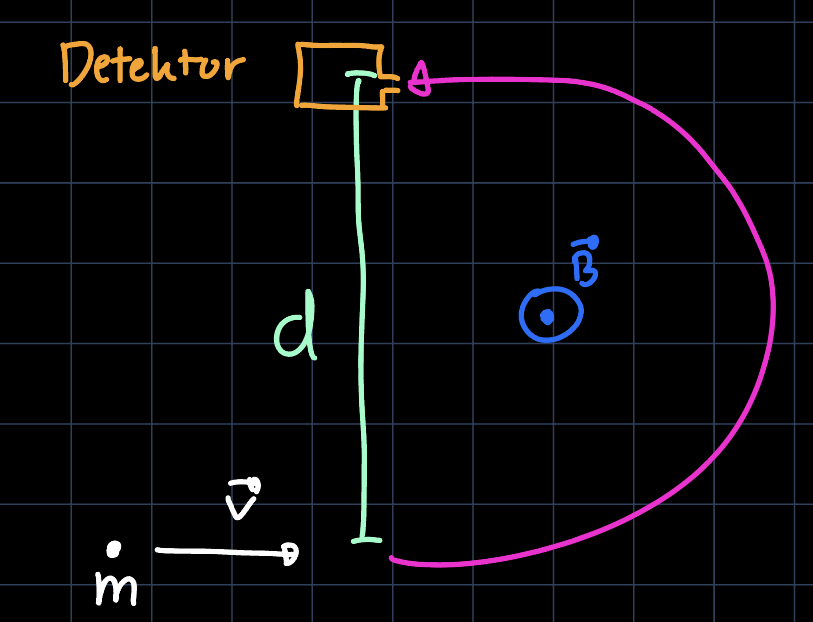
Wir betrachten einen Massenspektrometer, wie in der untenstehenden Skizze illustriert. Ein Teilchen, welches zuvor auf $150\, \mathrm{m/s}$ beschleunigt wurde, trägt die Ladung $10\, \mathrm{nC}$ und wird durch ein Magnetfeld $B = 0.5\, \mathrm{T}$ (orthogonal zur Geschwindigkeit) abgelenkt und trifft auf einen Detektor, der $2\, \mathrm{m}$ weit weg platziert wurde. Bestimme die Masse des Teilchens.
Regression
Wir betrachten die Anzahl studierenden an der ETH über die letzten paar Jahre und wollen herausfinden, ob wir die Zahl für die Zukunft vorhersagen können. Dazu haben wir folgende Daten (Quelle):
| Jahr | Anzahl Studierende |
|---|---|
| 2016 | 18780 |
| 2017 | 19512 |
| 2018 | 20282 |
| 2019 | 21100 |
| 2020 | 22461 |
| 2021 | 23401 |
| 2022 | 23963 |
Überlege, welchen Zusammenhang du zwischen den beiden Grössen vermutest und normalisiere die Daten, so dass du eine lineare Regression durchführen kannst. Bestimme die Steigung und den y-Achsenabschnitt der Regressionsgeraden und gib die Gleichung der Geraden an. Berechne dann die Anzahl Studierende für das Jahr 2023 und wir werden Ende Semester sehen, wer die beste Vorhersagung getroffen hat.
Lösungen
Lösung schwebendes Wasser
Zuerst berechnen wir die auf den Wassertropfen wirkende Gravitationskraft:
$$F_G = m g = \frac{4}{3} \pi r^3 \rho g$$
Nun können wir die benötigte elektrische Kraft berechnen:
$$F_E = q E = 10\, \mathrm{nC} \cdot E$$
Damit der Tropfen schwebt, muss die elektrische Kraft gleich gross sein wie die Gravitationskraft:
$$F_E = F_G \Rightarrow q E = \frac{4}{3} \pi r^3 \rho g \Rightarrow E = \frac{4}{3} \pi r^3 \rho g / q = 513.47... \, \mathrm{N/C} \approx 510\, \mathrm{V/m}$$
Kommentar zur Einheit: Da per Def. $\mathrm{V} = \mathrm{J/C}$ folgt die letzte Umformung.
Lösung Beschleunigung im Plattenkondensator
$\Delta E = q U = 1.602176634 \cdot 10^{-19}\, \mathrm{C} \cdot 100\, \mathrm{V} = 1.602176634 \cdot 10^{-17}\, \mathrm{J}$
Lösung Massenspektrometer
Es wirken hier zwei Kräfte: Die Lorentzkraft $F_L = q v B$ und die Zentripetalkraft $F_Z = \frac{m v^2}{r}.$ Da die Zentripetalkraft die Lorentzkraft ausgleichen muss, gilt:
$$F_L = F_Z \Rightarrow q v B = \frac{m v^2}{r} \Rightarrow m = \frac{q v B r}{v^2} = \frac{q B r}{v} = \frac{10\, \mathrm{nC} \cdot 0.5\, \mathrm{T} \cdot 1\, \mathrm{m}}{150\, \mathrm{m/s}} \approx 3.33\cdot 10^{-11} \, \mathrm{kg}$$
Lösung Regression
Die Beschreibung hier bezieht sich auf die untenstehende Tabelle. Wir ergänzen die Tabelle erst einmal mit einer Spalte für die Differenz zum letzten Jahr.
| Jahr | Anzahl Studierende | Differenz |
|---|---|---|
| 2016 | 18780 | - |
| 2017 | 19512 | 732 |
| 2018 | 20282 | 770 |
| 2019 | 21100 | 818 |
| 2020 | 22461 | 1361 |
| 2021 | 23401 | 940 |
| 2022 | 23963 | 562 |
Die Differenz zeigt, dass eine Zunahme stattfindet und dann wieder eine Abnahme -> parabolischer Funktionsgraph ($f(x) = a x^2 + b x + c$). Setzten wir den Nullpunkt beim maximalen Wert vom Jahr 2020, so erhalten wir 'gratis' den Parameter $c = 1361$, welchen wir gleich abziehen und die Differenz davon betrachten. Nun suchen wir also eine Funktion $g(x) = a x^2 + b x.$ Diese können wir durch $x$ dividieren und erhalten so unseren Ansatz für eine lineare Regression mit den Daten in den zwei letzten Spalten der untenstehenden Tabelle:
| Jahr | Anzahl Studierende | Differenz | Differenz zu 1361 | Normierte Jahreszahl | Differenz durch Jahreszahl |
|---|---|---|---|---|---|
| 2017 | 19512 | 732 | -629 | -3 | 210 |
| 2018 | 20282 | 770 | -591 | -2 | 296 |
| 2019 | 21100 | 818 | -543 | -1 | 543 |
| 2021 | 23401 | 940 | -421 | 1 | -421 |
| 2022 | 23963 | 562 | -799 | 2 | -400 |
Nun können wir die lineare Regression durchführen und erhalten die Gleichung $g(x) = -165 x - 54.$ Machen wir die vorherigen Schritte rückwärts, so ergibt sich für die Differenz $f(x) = -165 x^2 - 54 x + 1361.$ Für das Jahr 2023 erhalten wir also $f(3) = 1361 - 165 \cdot 3^2 - 54 \cdot 3 = 1361 - 1485 - 162 = - 286$, womit wir eine Zunahme von $562 - 286 = 276$ Studierenden haben. Also erwarten wir nach dieser Vorhersage $23963 + 276 = 24239$ Studierende im Jahr 2023. Mal schauen wie gut das hinkommt xD.
Woche 3 - Drehimpuls - Klassisch und QM
Recap Vorlesung
Kurzes Beispiel Einheiten
Wieso ist es wichtig die Einheiten in einer Rechnung zu beachten? Folgendes Beispiel soll zeigen, wo es euch quasi die Lösung gibt. Wir möchten die Periode $T$ (=Schwingungsdauer) eines Federpendels bestimmen. Dabei wissen wir, dass diese von der Gravitationsbeschleunigung $g$, der Länge $l$ und der Masse $m$ des Pendels abhängen kann. Betrachten wir die Einheiten dieser Grössen, so erkennen wir: $[g] = \mathrm{m/s^2}$, $[l] = \mathrm{m}$ und $[m] = \mathrm{kg}$, sowie die gesuchte Grösse $[T] = \mathrm{s}$. Wir können nun versuchen eine Formel zu finden, die diese Grössen kombiniert und die richtige Einheit hat. Damit erkennen wir direkt $T \propto \sqrt{g l / m},$ womit wir das Problem gelöst haben.
Drehimpuls
Der Drehimpuls eines Objektes mit Impuls $\vec p$ und Ortsvektor $\vec r$ bezüglich einem Bezugspunkt (meist Koordinatenursprung $(0,0,0)$), ist definiert als $\vec L = \vec r \times \vec p.$ In den meisten Fällen betrachten wir ein einfaches System zweier Punktmassen wobei $\vec p$ und $\vec r$ orthogonal (rechtwinklig/senkrecht) zueinander stehen. Dann vereinfacht sich die Formel zu $L = r p$ (mit jeweils dem Betrag der Grössen).
Der Drehimpuls ist eine Erhaltungsgrösse. Das heisst, solange kein Drehmoment wirkt, bleibt der Drehimpuls konstant: Wenn sich ein Objekt dreht, dreht es sich immer gleich schnell weiter. Das ist auch der Grund, weshalb ein Kreisel aufrecht stehen kann oder ein Fahrrad sich von alleine aufrichtet.
Spin
Mit Spin wird der intrinsische Drehimpuls eines Teilchens bezeichnet. Er ist eine Eigenschaft des Teilchens und kann nicht verändert werden. Er ist ein quantenmechanisches Phänomen und kann nur durch die Quantenmechanik erklärt werden. Für euch reicht die Erklärung für den Spin eines Elektrons: "Electron spin in short: Imagine a ball that’s rotating, except it’s not a ball and it’s not rotating".
Aufgaben
Coulomb vs. Gravitationskraft
Wir betrachten ein System aus zwei gleichen Objekten der Masse $m$ und Ladung $q$, die sich in Distanz $r$ voneinander entfernt befinden. Berechne den Koeffizienten $m/q$, bei dem die Coulomb-kraft und die Gravitationskraft gleich gross sind. Ist dieser vom Abstand $r$ abhängig? Die Gravitationskonstante beträgt $G = 6.674 \cdot 10^{-11}\, \mathrm{m^3\,kg^{-1}\,s^{-2}}$ und die elektrische Feldkonstante $\varepsilon_0 = 8.854 \cdot 10^{-12}\, \mathrm{m^{-3}\,kg^{-1}\,s^4\,A^2}.$
Drehimpuls Quantenzahlen (Prüfung HS13)
Die natürlich vorkommenden Isotope von Magnesium sind $^{24} \mathrm{Mg}$, $^{25} \mathrm{Mg}$ und $^{26} \mathrm{Mg}.$ Erstelle eine Tabelle mit den Neutronen-, Protonen- und Elektronenzahlen der Isotope und gebe jeweils an, ob die Kernspindrehimpulsquantenzahl null, ganzzahlig oder halbganzzahlig ist.
Neon-Kombo (Prüfung FS20)
Basierend auf der nachfolgenden Tabelle, berechne die natürliche Häufigkeit aller möglichen Isotopomere des Neon-Dimers $\mathrm{Ne}_2$ (z.B. $^{20}\mathrm{Ne}-^{20}\mathrm{Ne}$).
| Isotop | Masse (u) | natürliche Häufigkeit |
|---|---|---|
| $^{20} \mathrm{Ne}$ | 19.99244 | 90.48% |
| $^{21} \mathrm{Ne}$ | 20.99384 | 0.27% |
| $^{22} \mathrm{Ne}$ | 21.99138 | 9.25% |
Magnetische Drehimpulsquantenzahl (Prüfung FS20)
$^{21}\mathrm{Ne}$ hat die Kernspindrehimpulsquantenzahl $I = 3/2.$ Gib alle möglichen Werte der magnetischen Kernspindrehimpulsquantenzahl $m_I$ an.
Kanonen-betriebenes Pendel (!SCHWIERIG!)
Wir betrachten eine Kanone, die eine Metallkugel der Masse $m = 10\, \mathrm{kg}$ mit einer Geschwindigkeit von $v = 100\, \mathrm{m/s^2}$ auf einen ruhenden Holzblock abfeuert, so dass die Kugel im Holzblock stecken bleibt. Der Holzblock ist an einer (angenommen Massenlosen) Schnur an der Decke aufgehängt (im Gravitationsfeld der Erde, $g = 9.81\, \mathrm{m/s}$) und schwingt nach dem Einschlag der Kugel mit einer Amplitude von $A = 0.1\, \mathrm{m} (vertikal).$ Berechne die Masse $M$ des Holzblockes.
Für die ganz motivierten: Angenommen das Pendel was ursprünglich $r = 1 \, \mathrm{m}$ lang und wurde nun auf $r' = 0.2\, \mathrm{m}$ gekürzt. Wie viel Energie musste dafür aufgewendet werden? Wie gross ist die Amplitude des Pendels jetzt?
Lösungen
Lösung Coulomb vs. Gravitationskraft
Die Gravitationskraft ist gegeben durch
$$F_G(r) = G \frac{m^2}{r^2}$$
und die Coulomb-kraft durch
$$F_{C}(r) = \frac{1}{4 \pi \varepsilon_0} \frac{q^2}{r^2}$$
Setzen wir diese gleich, erhalten wir
$$G \frac{m^2}{r^2} = \frac{1}{4 \pi \varepsilon_0} \frac{q^2}{r^2}$$
und nach $m/q$ aufgelöst
$$\frac{m}{q} = \sqrt{\frac{1}{4 \pi \varepsilon_0 G}} \approx 1.16 \cdot 10^{10} \, \mathrm{kg/C}$$
Wir sehen, dass das Masse zu Ladungs-Verhältnis riesig sein muss, damit die Gravitationskraft die Coulomb-kraft überwiegt. Die Distanz $r$ spielt keine Rolle, da beide Kräfte in gleicher Weise davon abhängig sind.
Lösung Drehimpuls Quantenzahlen
Die Anzahl Protonen und Elektronen ist für neutrale Teilchen gleich der Ordnungszahl, also hier überall $12.$ Die Anzahl Neutronen ergibt sich aus der Differenz zwischen Massenzahl und Ordnungszahl. Die Kernspindrehimpulsquantenzahl ist null, falls die Anzahl Neutronen und Protonen beide gerade sind, ganzzahlig falls beide ungerade und halbganzzahlig falls nur eine der beiden ungerade ist oder (äquivalente Bedingung) die Massenzahl ungerade ist. Damit ergibt sich die Tabelle:
| Isotop | # Neutronen | # Protonen | # Elektronen | I |
|---|---|---|---|---|
| $^{24} \mathrm{Mg}$ | 12 | 12 | 12 | 0 |
| $^{25} \mathrm{Mg}$ | 13 | 12 | 12 | halbganzzahlig |
| $^{26} \mathrm{Mg}$ | 14 | 12 | 12 | 0 |
Lösung Neon-Kombo
Die Häufigkeit eines Isotopomers ergibt sich aus dem Produkt der Häufigkeiten der beiden Isotope. Achtung: Bei Isotopomeren zweier verschiedenen Isotopen muss das Produkt noch verdoppelt werden, da die Reihenfolge keine Rolle spielt. Damit ergibt sich die Tabelle:
| Isotopomer | Häufigkeit |
|---|---|
| $^{20} \mathrm{Ne}-^{20} \mathrm{Ne}$ | 0.8187 |
| $^{20} \mathrm{Ne}-^{21} \mathrm{Ne}$ | 0.0049 |
| $^{20} \mathrm{Ne}-^{22} \mathrm{Ne}$ | 0.1674 |
| $^{21} \mathrm{Ne}-^{21} \mathrm{Ne}$ | $7.3\cdot 10^{-6}$ |
| $^{21} \mathrm{Ne}-^{22} \mathrm{Ne}$ | 0.0005 |
| $^{22} \mathrm{Ne}-^{22} \mathrm{Ne}$ | 0.0086 |
Lösung Magnetische Drehimpulsquantenzahl
Die möglichen Werte sind $m_I = -I, -I + 1, \ldots, I - 1, I.$ Also in diesem Fall $m_I = -3/2, -1/2, 1/2, 3/2.$
Lösung Kanonen-betriebenes Pendel
Die Aufgabe lässt sich sehr schön über Impuls und anschliessender Energieerhaltung lösen.
Der Impuls der Kugel $p = m v$ wird vollständig auf das neue System aus Holzblock und Kugel übertragen, da er erhalten bleibt. Also gilt $p = m v = (M + m) v'$, wobei $v'$ die Geschwindigkeit des Systems nach dem Einschlag ist. Mit der Energieerhaltung der angeregten Schwingung des Systems, die eine Amplitude von $A$ und damit eine Veränderung der potentiellen Energie von $\Delta E_\textrm{pot} = m g A$ hat, erhalten wir:
$$\frac{1}{2} (M + m) v'^2 = (M + m) g A$$
Setzen wir den Impulsausdruck für $v'$ ein, erhalten wir:
$$\frac{1}{2} (M + m) \left(\frac{m v}{M + m}\right)^2 = (M + m) g A$$
Auflösen nach $M$ ergibt:
$$M = \frac{m v}{\sqrt{2 g A}} - m \approx 704\, \mathrm{kg}$$
Dies ist etwa ein sinnvolles Gewicht, wenn man betrachtet, dass die Kugel mit $100\, \mathrm{m/s} = 360\, \mathrm{km/h}$ auf den Holzblock trifft.
Für die ganz motivierten: Hier geht es darum die Drehimpulserhaltung anzuwenden. In der Gleichgewichtsposition hat das Pendel den Drehimpuls.
$$L = (M + m) r v'$$
Wenn nun die Schnur verkürzt wird, muss das Pendel schneller rotieren, damit der Drehimpuls erhalten bleibt. Es muss also
$$(M + m) r v' = (M + m) r' v''$$
gelten, womit nach $v''$ aufgelöst
$$v'' = \frac{r}{r'} v'$$
folgt. Die dafür aufzuwendende Energie ist gegeben durch die Differenz der kinetischen Energien in Gleichgewichtslage
$$\Delta E_\textrm{kin} = \frac{1}{2} (M + m) v''^2 - \frac{1}{2} (M + m) v'^2 = \frac{1}{2} (M + m) v'^2 \left(\frac{r^2}{r'^2} - 1\right) \approx 2.8\, \mathrm{kJ}$$
Betrachten wir noch einmal die Energieerhaltung mit potentieller Energie
$$E_\textrm{pot,max} = m g A' = E_\textrm{kin,max} = \frac{1}{2} (M + m) v''^2$$
ergibt sich die neue Amplitude des Pendels durch
$$A' = \frac{E_\textrm{kin,max}}{m g} \approx 36.7\, \mathrm{m}$$
Diese Zahl ist nun aber mehr als doppelt so gross wie die Länge des Pendels! Es wird also eine Kreisbewegung in eine Richtung, die oben etwas langsamer ist als unten geben und die 'echte Amplitude' ist nur $A = 2 \cdot r' = 0.4\, \mathrm{m}.$
Woche 4 - Massendefekt & Radioaktive Zerfälle
Massendefekt
Wenn ein Atomkern aus seinen Elementarteilchen gebildet wird, geht dabei Masse verloren (rechne mal nach!). Dies ist eine gute Demonstration der Formel für die durch Massenverlust freigesetzte Energie: $\Delta E = \Delta m c^2.$ Genau dies wird auch bei Kernkraftwerken ausgenutzt; mehr dazu in den Übungen.
Radioaktive Zerfälle
Wird bei einem physikalischen oder chemischen Prozess Energie frei, so bezeichnet man ihn als spontan, respektive die Ausgangsstoffe als instabil. Der Massendefekt zeigt uns, dass einige Atomkerne instabil sind und unter freisetzung von Energie zerfallen. Die wichtigsten Zerfallsarten sind:
- $\alpha$-Zerfall: Ein Heliumkern $(\mathrm{^{4}He^{2+}})$ wird aus dem Atomkern ausgestossen.
- $\beta^-$-Zerfall: Ein Neutron zerfällt zu einem Proton $(\mathrm{p}^+)$, einem Elektron $(\mathrm{e}^-)$ und einem Antineutrino $(\bar{\nu}_e)$
- $\beta^+$-Zerfall: Ein Proton zerfällt zu einem Neutron $(\mathrm{n}^0)$, einem Positron $(\mathrm{e}^+)$ und einem Neutrino $(\nu_e)$
Vergesst nicht die Ladung beim aufschreiben der Reaktionsgleichung (z.B. beim $\alpha$-Zerfall ist der entstehende Kern zweifach negativ geladen)! Die weiteren Zerfälle sind für uns nicht relevant.
Voraussage Zerfallsart
Die Zerfallsart kann (mühsam) in einer Nuklidkarte nachgeschlagen werden, aber auch (keine Garantie auf Richtigkeit!) schnell vorausgesagt werden: Nimm ein Periodensystem zur Hand und schau die drei möglichen Produkte an. Das Produkt, bei dem die Masse am nächsten bei der im Periodensystem angegebenen Masse liegt, ist meistens das richtige.
Kinetik radioaktiver Zerfälle
Atomkerne zerfallen mit einer gewissen Wahrscheinlichkeit. Damit können wir erkennen, dass die Abnahmerate proportional zur Anzahl Atomkerne sein muss und erhalten die Differentialgleichung:
$$\dd{N(t)}{t} = -k N(t)$$
Die Lösung dieser Differentialgleichung ist:
$$N(t) = N_0 e^{-kt}$$
Wobei $k$ die Zerfallskonstante bezeichnet. Oft wird die Zerfallsrate auch in Form der Halbwertszeit angegeben, die Zeit in der die Hälfte der Kerne zerfallen ist. Setzten wir dies in unser Zeitgesetz ein, erhalten wir:
$$\frac{N_0}{2} = N_0 e^{-kt_{1/2}} \Rightarrow t_{1/2} = \frac{\ln 2}{k}$$
Oder wenn wir die Zerfallskonstante erhalten möchten:
$$k = \frac{\ln 2}{t_{1/2}}$$
Aktivität
Die Aktivität $A$ ist definiert als die Anzahl Zerfälle pro Sekunde. Wir können sie also einfach aus der Ableitung der Anzahl Atomkerne nach der Zeit berechnen (wird den Studenten überlassen). Die gebräuchliche Einheit der Aktivität ist das Becquerel ($\mathrm{Bq}$ = $\mathrm{s}^{-1}$, Anzahl Zerfälle pro Sekunde).
Beispiele von Aufgaben
Massendefekt (Prüfung HS21)
Die Masse von $\mathrm{^{240}Pu}$ beträgt $240.0538135\, \mathrm{u}.$ Berechne den Massendefekt in Joule bei der Bildung von $_{94}^{240} \mathrm{Pu}$ aus Protonen, Neutronen und Elektronen.
Voraussage radioaktive Zerfälle
Die folgenden radioaktiven Kerne zerfallen zu mehr oder weniger stabilen Kernen. Gib jeweils die Zerfallsart und eine vollständige Zerfallsgleichung an.
- $\mathrm{^{14}C}$
- $\mathrm{^{190}Ir}$
- $\mathrm{^{211}Po}$
- $\mathrm{^{40}K}$
- $\mathrm{^{195}Hg}$
Radioaktivität in der Medizin
In der Medizin werden radioaktive Isotope für verschiedene Zwecke eingesetzt. Ein Beispiel ist die Positronen-Emissions-Tomographie (PET), bei der radioaktive Isotope in den Körper gespritzt werden, die sich in bestimmten Organen anreichern [^1]. Die Strahlung, die von den Isotopen ausgesendet wird, kann dann von aussen gemessen werden und gibt Aufschluss über die Verteilung des Isotops im Körper. Ein Beispiel für ein solches Isotop ist $\mathrm{^{18}F},$ das durch $\beta^+$-Zerfall in $\mathrm{^{18}O}$ zerfällt. Die Halbwertszeit von $\mathrm{^{18}F}$ beträgt $109.8\, \mathrm{min}.$
a) Gib die Reaktionsgleichung für den Zerfall von $\mathrm{^{18}F}$ an.
b) Berechne die Zerfallskonstante $k$ von $\mathrm{^{18}F}.$
c) Berechne die Aktivität von $1.0\, \mathrm{g}$ $\mathrm{^{18}F}$ nach $5.0\, \mathrm{min}.$
d) Wie viel $\mathrm{^{18}F}$ muss für eine Untersuchung mit einer Aktivität von $1.0\, \mathrm{MBq}$ gespritzt werden, wenn die Untersuchung $5\, \mathrm{min}$ nach der Infusion startet? $(\text{in}\, \mathrm{mg})$
e) Wie viel $\mathrm{^{18}F}$ wird insgesamt benötigt, wenn wir die Aktivität konstant auf $1.0\, \mathrm{MBq}$ halten möchten für eine Untersuchung von $t = 30\, \mathrm{min}$? $(\text{in}\, \mathrm{mg})$
Lösungen
Lösung Massendefekt
Der Massendefekt kann durch die Formel $\Delta m = m - Z m_{\mathrm{p}} - N m_{\mathrm{n}} - Z m_{\mathrm{e}}$ berechnet werden. Dabei ist $m$ die Masse des Atomkerns, $Z$ die Anzahl Protonen, $N$ die Anzahl Neutronen und $m_{\mathrm{p}}, m_{\mathrm{n}}$ und $m_{\mathrm{e}}$ die Massen von Proton, Neutron und Elektron. Der Energieunterschied ergibt sich dann durch $\Delta E = \Delta m c^2.$
$$\Delta m = 240.0538135\, \mathrm{u} - 94 \cdot 1.00727647\, \mathrm{u} - 146 \cdot 1.00866492\, \mathrm{u} - 94 \cdot 0.00054858\, \mathrm{u} \approx -1.9466\, \mathrm{u}$$
$$\Delta E = m c^2 \approx -2.905 \cdot 10^{-10} \, \mathrm{J}$$
Das negative Vorzeichen bedeutet, dass Energie frei wird. Es spielt aber keine Rolle, wenn es nicht vorhanden ist, solange euch klar ist, dass Energie frei wird.
Lösung Voraussage radioaktive Zerfälle
- $\mathrm{^{14}C}$
$$\mathrm{\beta^--Zerfall}: \quad \mathrm{^{14}C} \rightarrow \mathrm{^{14}N^+} + \mathrm{e}^- + \bar{\nu}_e$$
- $\mathrm{^{190}Ir}$
$$\mathrm{\beta^+-Zerfall}: \quad \mathrm{^{190}Ir} \rightarrow \mathrm{^{190}Os^-} + \mathrm{e}^+ + \nu_e$$
-
$\mathrm{^{211}Po}$
$$\mathrm{\alpha-Zerfall}: \quad \mathrm{^{211}Po} \rightarrow \mathrm{^{207}Pb^{2-}} + \mathrm{^{4}He^{2+}}$$
-
$\mathrm{^{40}K}$
$$\mathrm{\beta^--Zerfall}: \quad \mathrm{^{40}K} \rightarrow \mathrm{^{40}Ca^+} + \mathrm{e}^- + \bar{\nu}_e$$
-
$\mathrm{^{195}Hg}$
$$\mathrm{\beta^+-Zerfall}: \quad \mathrm{^{195}Hg} \rightarrow \mathrm{^{195}Au^-} + \mathrm{e}^+ + \nu_e$$
Lösung Radioaktivität in der Medizin
a) $\mathrm{^{18}F} \rightarrow \mathrm{^{18}O} + \mathrm{e}^+ + \nu_e$
b) $k = \frac{\ln 2}{t_{1/2}} = \frac{\ln 2}{109.8\, \mathrm{min}} \approx 1.052 \cdot 10^{-4}\, \mathrm{s^{-1}}$
c) Zuerst berechnen wir die Anzahl Atomkerne $N_0$ in $1.0\, \mathrm{mg}$ $\mathrm{^{18}F}.$
$$N_0 = \frac{1.0\, \mathrm{g}}{18.0\, \mathrm{g/mol}} \cdot {6.022 \cdot 10^{23}}\mathrm{mol^{-1}} \approx 3.3 \cdot 10^{22}$$
Die Anzahl radioaktiver Kerne nimmt exponentiell ab mit der Zeit. Dies kann durch die Formel $N(t) = N_0 e^{-kt}$ beschrieben werden. Die Aktivität ist definiert als die Anzahl Zerfälle pro Sekunde. Somit ergibt sich:
$$A(t) = -\dd{N(t)}{t} = -\dd{N_0 e^{-kt}}{t} = k N_0 e^{-kt}$$
Und nach einsetzen der gegebenen Werte:
$$A(5\, \mathrm{min}) \approx 3.41 \cdot 10^{18} \, \mathrm{Bq}$$
d) Da die Aktivität proportional zur ursprünglichen Anzahl radioaktiver Kerne ist, können wir einfach unser Ergebnis aus c) benutzen und erhalten:
$$m_{\mathrm{^{18}F}} = \frac{1.0\, \mathrm{MBq}}{3.41 \cdot 10^{18} \, \mathrm{Bq}} \cdot 1.0\, \mathrm{mg} \approx 2.93 \cdot 10^{-13}\, \mathrm{mg}$$
e) Damit die Aktivität konstant bleibt, muss jederzeit gerade so viel $\mathrm{^{18}F}$ gespritzt werden, wie verbraucht wird. Die Definition der Aktivität gibt uns an, wie viele Zerfälle pro Sekunde stattfinden. Wir können diese Zahl also einfach mit der Dauer der Untersuchung multiplizieren, um das durch den Zerfall verbrauchte $\mathrm{^{18}F}$ zu erhalten. Dazu kommt noch der Verbrauch aus c). Insgesamt ergibt sich:
$$m_{\mathrm{^{18}F, cst.}} = t A + m_{\mathrm{^{18}F}} \approx 30\, \mathrm{min} 1.0\, \mathrm{MBq} 18.0\, \mathrm{u} + 2.93 \cdot 10^{-13}\, \mathrm{mg} \approx 5.41 \cdot 10^{-17} \, \mathrm{kg}$$
Quellen
Woche 5 - Radioaktive Zerfälle & Zerfallsketten
Theorie
Zerfallsarten und Zerfallsgleichungen
$\alpha$-Zerfall
Bei einem $\alpha$-Zerfall wird ein Heliumkern ($\mathrm{^{4}He}$) aus dem Kern eines Atoms ausgestossen. Dabei wird die Massenzahl um $4$ und die Ordnungszahl um $2$ verringert. Bsp. für einen $\alpha$-Zerfall:
$$ _{88}^{224}{\rm{Ra}} \rightarrow _{86}^{220}{\rm{Rn}^{2-}} + _2^4{\rm{He}^{2+}} $$
Credit: Leifiphysik
$\beta^-$-Zerfall
Beim $\beta^-$-Zerfall wird ein Elektron aus dem Kern eines Atoms ausgestossen. Dabei wird die Ordnungszahl um $1$ erhöht. Bsp. für einen $\beta^-$-Zerfall:
$$ _{82}^{214}{\rm{Pb}} \rightarrow _{83}^{214}{\rm{Bi}^+} + {\rm{e}^-} + \bar {\rm{\nu_e}} $$
Credit: Leifiphysik
$\beta^+$-Zerfall
Beim $\beta^+$-Zerfall wird ein Positron aus dem Kern eines Atoms ausgestossen. Dabei wird die Ordnungszahl um $1$ verringert. Bsp. für einen $\beta^+$-Zerfall:
$$ _{6}^{11}{\rm{C}} \rightarrow _{5}^{11}{\rm{B}^-} + \bar{\rm{e}}^+ + {\rm{\nu_e}} $$
$\gamma$-Zerfall
Beim $\gamma$-Zerfall zerfällt ein Atomkern von einem angeregten Zustand in einen energetisch tieferen Zustand. Die dabei frei gewordene Energie wird in form von elektromagnetischer Strahlung abgegeben. Bsp. für einen $\gamma$-Zerfall:
$$ _{84}^{218}{\rm{Po}}^{\ast} \rightarrow _{84}^{218}{\rm{Po}} + {\rm{\gamma }} $$
Credit: Leifiphysik
Da es sich hier nicht wirklich um einen Zerfall handelt, spricht man häufig auch von einem $\gamma$-Übergang.
Folgen von Zerfallsreaktionen
Oft zerfallen radioaktive Kerne nicht direkt in stabile Kerne, sondern in instabile Zwischenprodukte, welche wiederum zerfallen. Dieser Prozess wird als Zerfallsreihe bezeichnet. Ein Beispiel für eine Zerfallsreihe ist die Zerfallsreihe von Uran (details siehe Skript):
$$ _{92}^{238}{\rm{U}} \rightarrow _{90}^{234}{\rm{Th^{2-}}} + _2^4{\rm{He^{2+}}} $$
$$ _{90}^{234}{\rm{Th}} \rightarrow _{91}^{234}{\rm{Pa^+}} + {\rm{e}}^- + \bar {\rm{\nu_e}} $$
$$ _{91}^{234}{\rm{Pa}} \rightarrow _{92}^{234}{\rm{U^+}} + {\rm{e}}^- + \bar {\rm{\nu_e}} $$
$$ _{92}^{234}{\rm{U}} \rightarrow _{90}^{230}{\rm{Th^{2-}}} + _2^4{\rm{He^{2+}}} $$
und so weiter bis zu einem stabilen Kern.
Kinetik von Folgereaktionen
Die Kinetik von Folgereaktionen kann mit einem System von gekoppelten Differentialgleichungen beschrieben werden. Betrachten wir die allgemeine Reaktion
$$ A \xrightarrow{k_A} B \xrightarrow{k_B} C \xrightarrow{k_C} \dots $$
so können wir die Anzahl der Kerne $A$, $B$, $C$, $\dots$ in Abhängigkeit der Zeit $t$ mit folgendem System von Differentialgleichungen beschreiben:
$$ \frac{{\rm{d}}{N_A}}{{\rm{d}}t} = - k_A N_A $$
$$ \frac{{\rm{d}}{N_B}}{{\rm{d}}t} = k_A N_A - k_B N_B $$
$$ \frac{{\rm{d}}{N_C}}{{\rm{d}}t} = k_B N_B - k_C N_C $$
und so weiter. Dabei ist $k_A$ die Zerfallskonstante von $A$, $k_B$ die Zerfallskonstante von $B$ und so weiter. Stell dir das so vor, dass die Änderung der Anzahl Kerne durch die Differenz der Produktions- und Abbaugeschwindigkeit gegeben ist.
Darstellung der Kinetik
Die Differentialgleichungen müsst ihr nicht lösen können, aber ihr solltet ein Gefühl dafür entwickeln, welchen Einfluss die Grösse der Zerfallskonstanten auf die Kinetik hat. Dazu schauen wir uns eine schöne Demonstration mit Wassergefässen in der ÜS an. Hier ist auch ein Video davon: Die erste Geschwindigkeitskonstante ist gross, die zweite ist klein und die dritte wieder gross. Dadurch leert sich das erste Gefäss schnell, das zweite wird anfangs aufgefüllt, bis es ein Maximum erreicht und nimmt dann (als geschwindigkeitsbestimmender Schritt) wieder ab. Im dritten Gefäss ist das enthaltene Volumen konstant sehr klein, da aufgrund der grossen Zerfallsgeschwindigkeit alles was darin entsteht sofort wieder zerfällt.
Ausserdem könnt ihr mit der Simulation unten ein bisschen spielen:
Aufgaben
Zerfallsreihe von $^{209}\mathrm{Pb}$
$^{209}_{82} \mathrm{Pb}$ zerfällt mit einem $\beta^-$-Zerfall zu einem instabilen Isotop, welches durch $\alpha$-Zerfall zu einem stabilen Kern zerfällt. Die Halbwertszeit von $^{209}\mathrm{Pb}$ beträgt $3.253\, \mathrm{h}$ und die Halbwertszeit des unbekannten Isotope beträgt $2.01 \cdot 10^{19}\, \mathrm{a}.$
a) Gib die (zwei) Reaktionsgleichungen die Zerfallsreihe von $^{209}\mathrm{Pb}$ an.
b) Berechne die Zerfallskonstanten der beiden Zerfälle.
c) Stelle die Differentialgleichungen für die Anzahl der Kerne aller vorkommenden Kerne in Abhängigkeit der Zeit an.
d) Erstelle ein qualitatives Diagramm für die Anzahl der vorkommenden Kerne in Abhängigkeit der Zeit in einem Zeitintervall von $0$ bis $1\, \mathrm{d}$,
e) sowie in einem Zeitintervall von $0$ bis $2 \cdot 10^{19}\, \mathrm{a}$.
f) Aus dem Skript ist eine allgemeine Formel für die Anzahl der Kerne in Abhängigkeit der Zeit für eine Zerfallsreihe gegeben:
$$T(1) \xrightarrow{^{k_1}} T(2) \xrightarrow{^{k_2}} \cdots \xrightarrow{^{k_N}} T(N+1)$$
$$N_{T(i)}(t) = N_{T(1)}(t=0) \prod_{n=1}^{i-1} k_n \sum_{l=1}^i \frac{\exp(-k_l(t))}{\prod_{j=1}^{l-1}(k_j-k_l) \prod_{j=l+1}^i (k_j-k_l)} $$
Verwende diese Formel, um die Anzahl der ersten beiden Kerne in Abhängigkeit der Zeit für die Zerfallsreihe von $^{209}\mathrm{Pb}$ zu berechnen. Überprüfe, ob deine Diagramme aus d) und e) mit dieser Formel übereinstimmen.
g) Zu welchem Zeitpunkt ist die Anzahl der Kerne des instabilen Isotops maximal? Wie gross ist der Anteil des instabilen Isotops zu diesem Zeitpunkt?
Lösungen
Lösung Zerfallsreihe von $^{209}\mathrm{Pb}$
a) Die gesuchten Zerfallsgleichungen lauten:
$$ _{82}^{209} \mathrm{Pb} \rightarrow ^{209}_{83} \mathrm{Bi^+} + e^- + \bar{\nu_e} $$
$$ _{83}^{209} \mathrm{Bi} \rightarrow ^{205}_{81} \mathrm{Tl^{2-}} + \mathrm{He^{2+}} $$
b) Die Zerfallskonstanten erhalten wir über die Formel
$$ k = \frac{\ln(2)}{t_{1/2}} $$
wobei $t_{1/2}$ die Halbwertszeit ist. Für $^{209}\mathrm{Pb}$ erhalten wir
$$ k_{^{209}\mathrm{Pb}} = \frac{\ln(2)}{3.253\, \mathrm{h}} \approx 5.919 \cdot 10^{-5}\, \mathrm{s^{-1}} $$
und für $^{209}\mathrm{Bi}$
$$ K_{^{209}\mathrm{Bi}} = \frac{\ln(2)}{2.01 \cdot 10^{19}\, \mathrm{a}} \approx 1.09 \cdot 10^{-27}\, \mathrm{s^{-1}} $$
c) Die Differentialgleichungen lassen sich aus den Reaktionsgleichungen aus a) finden:
$$ \frac{{\rm{d}}{N_{^{209}\mathrm{Pb}}}}{{\rm{d}}t} = - k_{^{209}\mathrm{Pb}} N_{^{209}\mathrm{Pb}} $$
$$ \frac{{\rm{d}}{N_{^{209}\mathrm{Bi}}}}{{\rm{d}}t} = k_{^{209}\mathrm{Pb}} N_{^{209}\mathrm{Pb}} - k_{^{209}\mathrm{Bi}} N_{^{209}\mathrm{Bi}} $$
$$ \frac{{\rm{d}}{N_{^{205}\mathrm{Tl}}}}{{\rm{d}}t} = k_{^{209}\mathrm{Bi}} N_{^{209}\mathrm{Bi}} $$
d) Innerhalb von einem Tag nimmt die Konzentration von $^{209}\mathrm{Pb}$ exponentiell auf
$$ 2^{-\frac{24 \mathrm{h}}{3.253 \mathrm{h}}} \approx 0.006 \approx 0 $$
ab, während die Konzentration von $^{209}\mathrm{Bi}$ exponentiell auf $\approx 1$ zunimmt. Die exponentielle Abnahme von $^{209}\mathrm{Bi}$ ist aufgrund der viel grösseren Halbwertszeit vernachlässigbar, womit auch vernachlässigbar wenig $^{205}\mathrm{Tl}$ entsteht. Ein qualitatives Diagramm sieht also wie folgt aus:
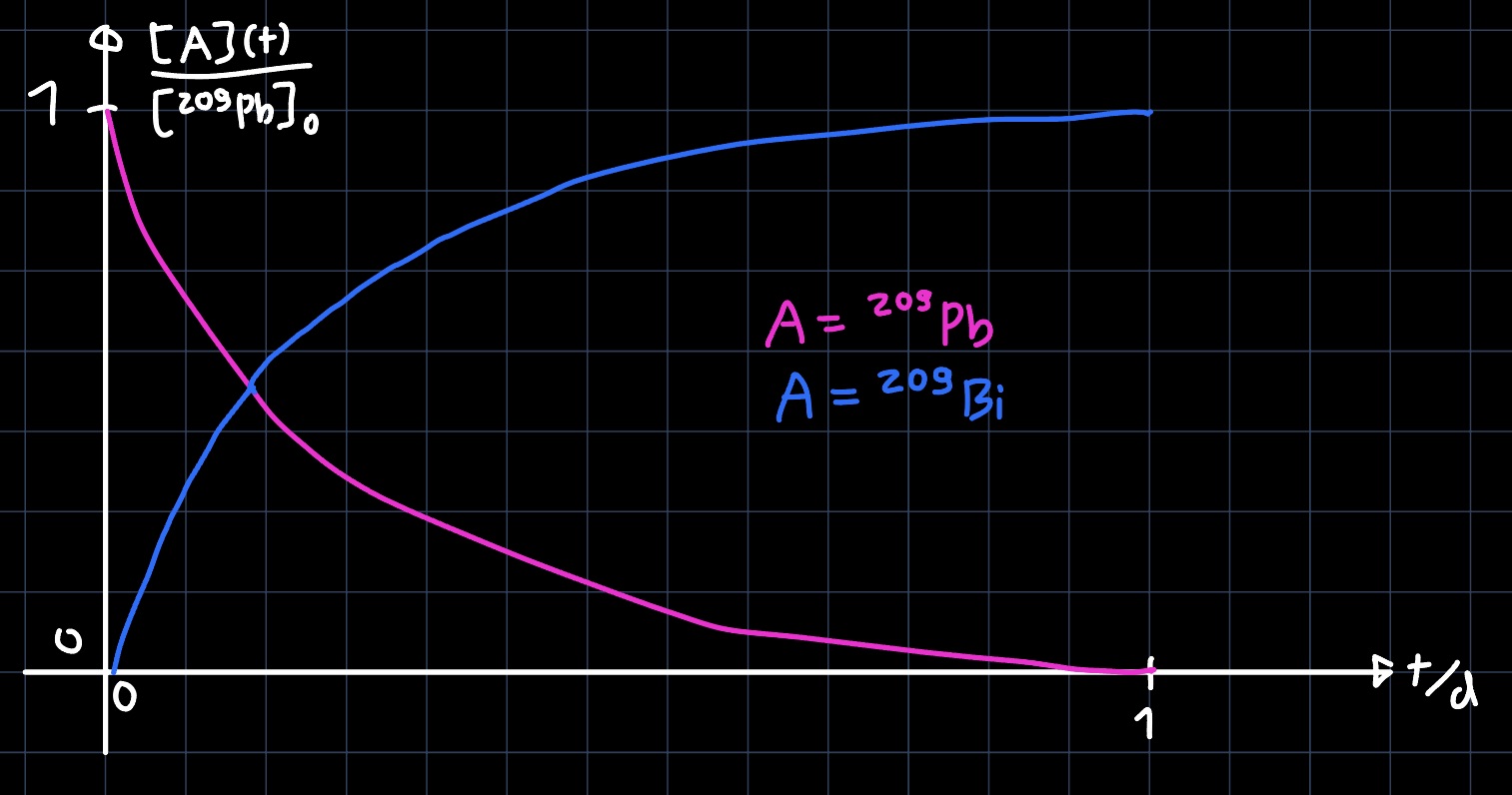
e) In der viel längeren Zeitskala ist die Halbwertszeit von $^{209}\mathrm{Pb}$ vernachlässigbar (es wird so gut wie alles zerfallen sein). Somit nimmt die Konzentration von $^{209}\mathrm{Bi}$ exponentiell ab, während die Konzentration von $^{205}\mathrm{Tl}$ exponentiell zunimmt. Ein qualitatives Diagramm sieht also wie folgt aus:
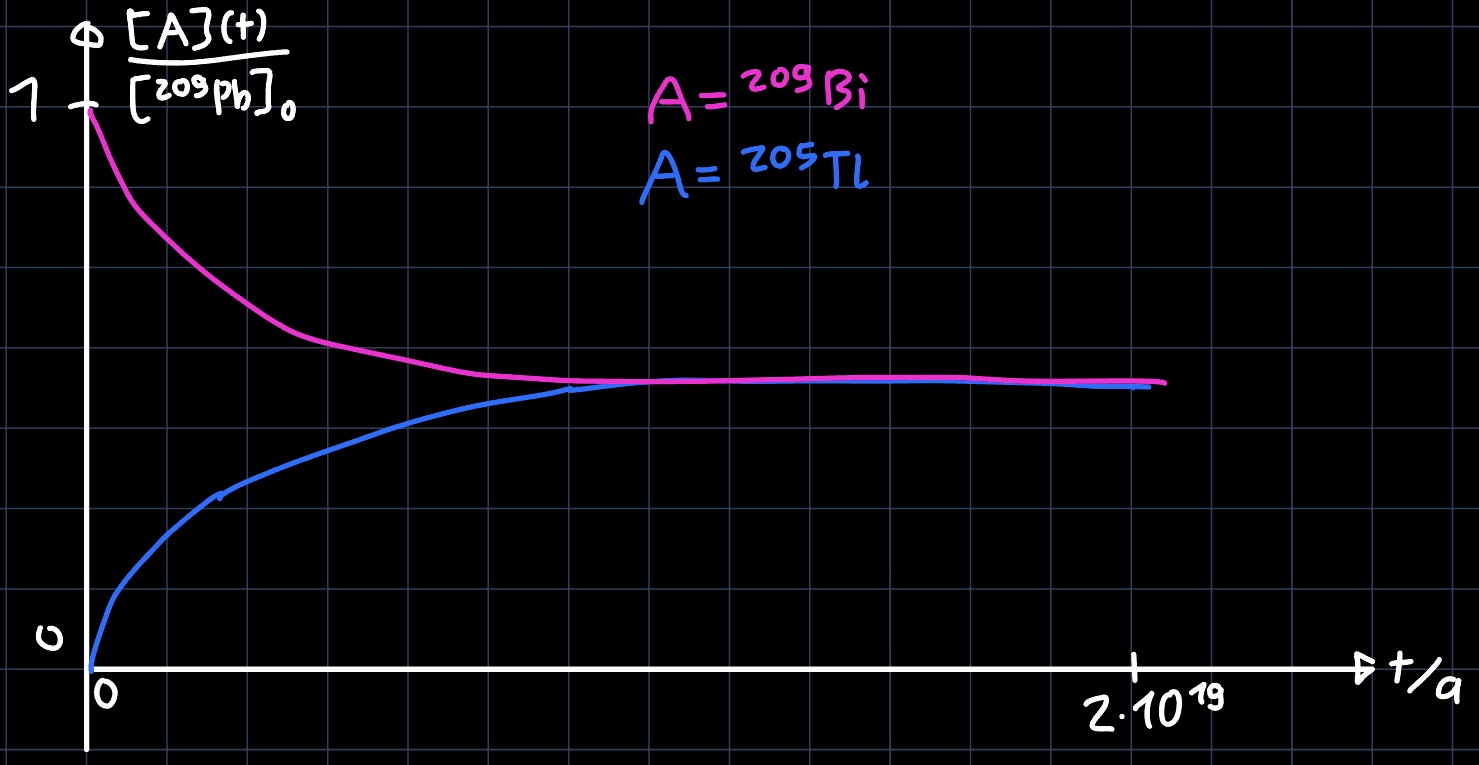
f) Einsetzen in die allgemeine Formel ergibt:
$$N_{^{209}\mathrm{Pb}}(t) = N_{^{209}\mathrm{Pb}}(t=0) \cdot \exp(-k_{^{209}\mathrm{Pb}} t)$$
$$ \begin{aligned} N_{^{209}\mathrm{Bi}}(t) &= N_{^{209}\mathrm{Pb}}(t=0) \cdot k_{^{209}\mathrm{Pb}}\left(\frac{\exp(-k_{^{209}\mathrm{Pb}} t)}{{k_{^{209}\mathrm{Bi}} - k_{^{209}\mathrm{Pb}}}} + \frac{\exp(-k_{^{209}\mathrm{Bi}} t)}{k_{^{209}\mathrm{Pb}} - k_{^{209}\mathrm{Bi}}}\right) \\ &= N_{^{209}\mathrm{Pb}}(t=0) \cdot \frac{k_{^{209}\mathrm{Pb}}}{k_{^{209}\mathrm{Bi}} - k_{^{209}\mathrm{Pb}}}\bigg(\exp(-k_{^{209}\mathrm{Pb}} t) - \exp(-k_{^{209}\mathrm{Bi}} t)\bigg) \end{aligned} $$
Dies stimmt mit den Diagrammen aus d) und e) überein, denn $k_{^{209}\mathrm{Pb}} \ll k_{^{209}\mathrm{Bi}}$.
g) Um die maximale Anzahl Kerne des instabilen Isotops zu bestimmen, müssen wir die Differentialgleichung für $N_{^{209}\mathrm{Bi}}$ nach $t$ ableiten und gleich null setzen:
$$ \begin{aligned} \frac{{\rm{d}}{N_{^{209}\mathrm{Bi}}}}{{\rm{d}}t} &= N_{^{209}\mathrm{Pb}}(t=0) \cdot \frac{k_{^{209}\mathrm{Pb}}}{k_{^{209}\mathrm{Bi}} - k_{^{209}\mathrm{Pb}}} \bigg( -k_{^{209}\mathrm{Pb}} \exp(-k_{^{209}\mathrm{Pb}} t) - -k_{^{209}\mathrm{Bi}} \exp(-k_{^{209}\mathrm{Bi}} t)\bigg) \\ & \propto k_{^{209}\mathrm{Pb}} \exp(-k_{^{209}\mathrm{Pb}} t) - k_{^{209}\mathrm{Bi}} \exp(-k_{^{209}\mathrm{Bi}} t) \end{aligned} $$
Daraus folgt
$$ t = \frac{1}{k_{^{209}\mathrm{Pb}} - k_{^{209}\mathrm{Bi}}} \ln\left(\frac{k_{^{209}\mathrm{Pb}}}{k_{^{209}\mathrm{Bi}}}\right) \approx 8.84 \cdot 10^5\, \mathrm{s} $$
und
$$ N_{^{209}\mathrm{Bi}}(t = 4.00 \cdot 10^{9}\, \mathrm{s}) \approx 1.0 \cdot N_{^{209}\mathrm{Pb}}(t = 0) $$
wie wir auch schon in e) gesehen haben.
Woche 6 - Kernspaltung & Energieproduktion
Theorie
Wir hatten nicht wirklich neue Theorie in der VL, aber ich möchte noch einen wichtigen Teil der Aufgabe von letzter Woche besprechen:
d) Innerhalb von einem Tag nimmt die Konzentration von $^{209}\mathrm{Pb}$ exponentiell auf
$$ 2^{-\frac{24 \mathrm{h}}{3.253 \mathrm{h}}} \approx 0.006 \approx 0 $$
ab, während die Konzentration von $^{209}\mathrm{Bi}$ exponentiell auf $\approx 1$ zunimmt. Die exponentielle Abnahme von $^{209}\mathrm{Bi}$ ist aufgrund der viel grösseren Halbwertszeit vernachlässigbar, womit auch vernachlässigbar wenig $^{205}\mathrm{Tl}$ entsteht. Ein qualitatives Diagramm sieht also wie folgt aus:

e) In der viel längeren Zeitskala ist die Halbwertszeit von $^{209}\mathrm{Pb}$ vernachlässigbar (es wird so gut wie alles zerfallen sein). Somit nimmt die Konzentration von $^{209}\mathrm{Bi}$ exponentiell ab, während die Konzentration von $^{205}\mathrm{Tl}$ exponentiell zunimmt. Ein qualitatives Diagramm sieht also wie folgt aus:

f) Aus dem Skript ist eine allgemeine Formel für die Anzahl der Kerne in Abhängigkeit der Zeit für eine Zerfallsreihe gegeben:
$$T(1) \xrightarrow{^{k_1}} T(2) \xrightarrow{^{k_2}} \cdots \xrightarrow{^{k_N}} T(N+1)$$
$$N_{T(i)}(t) = N_{T(1)}(t=0) \prod_{n=1}^{i-1} k_n \sum_{l=1}^i \frac{\exp(-k_l(t))}{\prod_{j=1}^{l-1}(k_j-k_l) \prod_{j=l+1}^i (k_j-k_l)} $$
Verwende diese Formel, um die Anzahl der ersten beiden Kerne in Abhängigkeit der Zeit für die Zerfallsreihe von $^{209}\mathrm{Pb}$ zu berechnen. Überprüfe, ob deine Diagramme aus d) und e) mit dieser Formel übereinstimmen.
Einsetzen in die Formel ergibt (und abkürzen von $k_{\mathrm{Pb}}$ durch $k_1$ und $k_{\mathrm{Bi}}$ durch $k_2$):
$$N_{1}(t) = N_{1}(t=0) \cdot \exp(-k_{1} t)$$
$$ \begin{aligned} N_{2}(t) &= N_{1}(t=0) \cdot k_{1}\left(\frac{\exp(-k_{1} t)}{{k_{2} - k_{1}}} + \frac{\exp(-k_{2} t)}{k_{1} - k_{2}}\right) \\ &= N_{1}(t=0) \cdot \frac{k_{1}}{k_{2} - k_{1}}\bigg(\exp(-k_{1} t) - \exp(-k_{2} t)\bigg) \end{aligned} $$
Wir erkennen die übereinstimmung mit dem Diagramm aus e), da die Zeit sehr gross ist verglichen mit der Zerfallskonstante von $\mathrm{^{209}Pb}$ und somit der Term die Anzahl $\mathrm{^{209}Pb}$ Kerne vernachlässigbar klein ist. Die Anzahl der $\mathrm{^{209}Bi}$ sinkt während der dargestellten Zeit exponentiell ab.
g) Zu welchem Zeitpunkt ist die Anzahl der Kerne des instabilen Isotops maximal? Wie gross ist der Anteil des instabilen Isotops zu diesem Zeitpunkt?
Um die maximale Anzahl Kerne des instabilen Isotops zu bestimmen, müssen wir die Differentialgleichung für $N_{2}$ nach $t$ ableiten und gleich null setzen:
$$ \begin{aligned} \frac{{\rm{d}}{N_{2}}}{{\rm{d}}t} &= N_{1}(t=0) \cdot \frac{k_{1}}{k_{2} - k_{1}} \bigg( -k_{1} \exp(-k_{1} t) - -k_{2} \exp(-k_{2} t)\bigg) \\ & \propto k_{1} \exp(-k_{1} t) - k_{2} \exp(-k_{2} t) \end{aligned} $$
Daraus folgt
$$ t = \frac{1}{k_{1} - k_{2}} \ln\left(\frac{k_{1}}{k_{2}}\right) \approx 8.84 \cdot 10^5\, \mathrm{s} $$
und
$$ N_{^{209}\mathrm{Bi}}(t = 4.00 \cdot 10^{9}\, \mathrm{s}) \approx 1.0 \cdot N_{^{209}\mathrm{Pb}}(t = 0) $$
wie wir auch schon in e) gesehen haben.
Aufgaben
Kernkraftwerk Gösgen-Däniken
In konventionellen Kernkraftwerken wird die Energie aus der Kernspaltung von Uran gewonnen. Dabei wird das Isotop $\mathrm{^{235}U}$ mit einem Neutron zu $\mathrm{^{89}Kr}$ und $\mathrm{^{144}Ba}$ gespalten, wobei zusätzlich drei Neutronen frei werden. Die Massen der beteiligten Atome sind:
$${m}\left( {_{{\mathrm{92}}}^{{\mathrm{235}}}{\mathrm{U}}} \right) = 235.04392996\, \mathrm{u}$$
$${m}\left( {_{\mathrm{0}}^{\mathrm{1}}{\mathrm{n}}} \right) = 1.00866492\, \mathrm{u}$$
$${m}\left( {_{{\mathrm{56}}}^{{\mathrm{144}}}{\mathrm{Ba}}} \right) = 143.92295281\, \mathrm{u}$$
$${m}\left( {_{{\mathrm{36}}}^{{\mathrm{89}}}{\mathrm{Kr}}} \right) = 88.91763058\, \mathrm{u}$$
a) Stelle eine Reaktionsgleichung für die beschriebene Kernspaltung von $\mathrm{^{235}U}$ auf. (Genau lesen!)
b) Berechne die Energie (in $\mathrm{kJ/mol})$, die bei der Reaktion frei wird.
c) Da Uran in der Natur nur zu $0.7\%$ aus $\mathrm{^{235}U}$ besteht, muss das Uran vor der Verwendung angereichert werden. Angereichertes Uran besteht zu $3.5\%$ aus $\mathrm{^{235}U}$ und zu $96.5\%$ aus $\mathrm{^{238}U}.$ Berechne die Energie, die pro $\mathrm{kg}$ angereichertem Uran bei der Kernspaltung freigesetzt wird.
d) Im Kernkraft Gösgen-Däniken wird Strom mit einer Leistung von rund $1.0\, \mathrm{GW}$ produziert [^1]. Wie viel angereichertes Uran $(\text{in} \, \mathrm{kg})$ muss dafür täglich angeliefert werden?
e) Tatsächlich wird täglich etwa $50\, \mathrm{kg}$ angereichertes Uran verbraucht (nach eigenen Angaben [^2]). Woher kommt der Unterschied zu deinem Resultat aus d)?
f) Betrachte nun ein Kohlekraftwerk, in dem Kohle $(\mathrm{C})$ zu $\mathrm{CO_2}$ umgewandelt wird. Gib eine Reaktionsgleichung für die Verbrennung von Kohle an.
g) Die Standardbildungsenthalpie von $\mathrm{CO_2}$ beträgt $\Delta H_B = -393\, \mathrm{kJ/mol}.$ Wie viel Kohle muss verbrannt werden, um die gleiche Energiemenge wie in d) in einem Tag produziert wird zu produzieren? (in mol) Nehme dafür an, das Kohlekraftwerk habe einen (hohen für Kohlekraftwerke) Wirkungsgrad von $45 \%$ [^3].
h) Wie viel $\mathrm{CO_2}$ Ausstoss wird demnach täglich durch den Betrieb des Kernkraftwerks Gösgen-Däniken eingespart? (in kg)
Kohle enthält natürlicherweise auch radioaktive Stoffe, genauer etwa $1\, \mathrm{ppm} \, ^{238}_{92}\mathrm{U}$ und $2\, \mathrm{ppm} \, ^{232}_{90}\mathrm{Th}$ [^4].
i) Berechne die Aktivität der radioaktiven Stoffe in der an einem Tag verbrannten Kohle. (in $\mathrm{Bq}$) Benutze dafür die Halbwertszeiten $t_{1/2}(^{238}\mathrm{U}) = 4.5 \cdot 10^9 \, \mathrm{a}$ und $t_{1/2}(^{232}\mathrm{Th}) = 1.4 \cdot 10^{10} \, \mathrm{a}.$
j) Nehme an die radioaktiven Stoffe bleiben in der Asche zurück und gelangen nicht mit dem Rauchgas in die Atmosphäre. Wieso ist die Stahlenbelastung von Kohle unproblematisch, während die Strahlenbelastung von der übrig bleibenden Asche ein Problem darstellt?
Das grosse Problem an der Strahlenbelastung durch Kohlenkraftwerke ist jedoch, dass die Asche nicht als Schadstoff behandelt wird, sondern häufig ungeschützt auf Deponien gelagert wird [^5]. Dadurch werden die radioaktiven Stoffe in die Umwelt freigesetzt und führen zu einer zusätzlichen Strahlenbelastung. Die Strahlenbelastung wird durch die effektive Dosis $D$ angegeben, die in $\mathrm{mSv}$ gemessen wird. Die effektive Dosis ist ein Mass für die biologische Wirkung der Strahlung. Die effektive Dosis kann über die Formeln:
$$D_{uran} = 1.53 \cdot 10^{-12} \, \frac{\mathrm{mSv/h}}{\mathrm{Bq/cm^3}} \frac{A}{V}$$
$$D_{thorium} = 2.06 \cdot 10^{-11} \, \frac{\mathrm{mSv/h}}{\mathrm{Bq/cm^3}} \frac{A}{V}$$
berechnet werden und verhält sich additiv. Dabei ist $A/V$ die Konzentration des jeweiligen Stoffes.
k) Nehme an, dass die radioaktiven Stoffe in der Asche zu $100\%$ (sinnvoll, da Gleichgewichtszustand) in eine Umgebung von $1\, \mathrm{km^3}$ freigesetzt werden. Berechne die zusätzliche Strahlenbelastung in $\mathrm{mSv/a}$ für die Umgebung. Das Kernkraftwerk Leibstadt verursacht nach eigenen Angaben eine Strahlenbelastung von maximal $0.01\, \mathrm{mSv/a}$ und produziert ähnlich viel Strom wie das oben betrachtete Kernkraftwerk Gösgen-Däniken [^6]. Verursacht also ein Kernkraftwerk oder ein Kohlekraftwerk mehr Strahlenbelastung?
Lösungen
Lösung Kernkraftwerk Gösgen-Däniken
a) Die gesuchte Reaktionsgleichung lautet:
$$\mathrm{^{235}U} + \mathrm{_0^1 n} \rightarrow \mathrm{^{89}Kr} + \mathrm{^{144}Ba} + 3\, \mathrm{_0^1 n}$$
b) Zuerst berechnen wir die Massendifferenz:
$$\Delta m = m\left( ^{{\mathrm{235}}}{\mathrm{U}} \right) - m\left( ^{{\mathrm{89}}}{\mathrm{Kr}} \right) - m\left( ^{{\mathrm{144}}}{\mathrm{Ba}} \right) - 2 m\left( ^{\mathrm{1}}{\mathrm{n}} \right) \approx 0.186\, \mathrm{u}$$
Einstein's Formel gibt uns dann die Energie:
$$\Delta E = \Delta m c^2 \approx 2.78 \cdot 10^{-11}\, \mathrm{J}$$
Und umgerechnet in $\mathrm{kJ/mol}$:
$$\Delta E \approx 1.67 \cdot 10^{10} \, \mathrm{kJ/mol}$$
c) Wir haben bereits die Energie pro Mol berechnet. Um die Energie pro $\mathrm{kg}$ zu erhalten, müssen wir durch die Molare Masse teilen:
$$\Delta E = \frac{120\, \mathrm{kJ/mol}}{235.04\dots \, \mathrm{g/mol}} = 7.11 \cdot 10^{13}\, \mathrm{J/kg}$$
Nun müssen wir noch den Anteil von spaltbarem $\mathrm{^{235}U}$ in angereichertem Uran berücksichtigen:
$$\Delta E = 7.11 \cdot 10^{10}\, \mathrm{kJ/g} \cdot 0.035 = 2.49 \cdot 10^{12} \, \mathrm{J/kg}$$
d) Eine Leistung von $1.0\, \mathrm{GW}$ bedeutet, dass pro Sekunde $1.0\, \mathrm{GJ}$ Energie produziert wird. Wir können nun die Energie pro Kilogramm aus c) verwenden, um die Masse Uran zu berechnen:
$$m_{\mathrm{U, theoretisch}} = \frac{1.0\, \mathrm{GW}}{2.49 \cdot 10^{12}\, \mathrm{J/kg}} \frac{86400 \mathrm{s}}{\mathrm{d}} \approx 34.7\, \mathrm{kg/d}$$
e) Der Unterschied kommt daher, dass das Kraftwerk keinen Wirkungsgrad von $100\%$ hat. Vergleichen wir die Zahlen können wir sogar den Wirkungsgrad des Kraftwerks abschätzen:
$$\eta = \frac{m_{\mathrm{U, theoretisch}}}{m_{\mathrm{U, real}}} \approx 63\%$$
f)
$$\mathrm{C} + \mathrm{O_2} \rightarrow \mathrm{CO_2}$$
g) In einem Tag werden
$$E = 1.0\, \mathrm{GW} \cdot 86400\, \mathrm{s/d} \approx 8.6 \cdot 10^{13}\, \mathrm{J/d}$$
produziert. Dafür benötigen wir
$$n_{\mathrm{C}} = -\frac{E}{\Delta H_B} \cdot \frac{1}{0.45} \approx 4.89 \cdot 10^8 \, \mathrm{mol}$$
h) Da die Reaktion stöchiometrisch ist, wird pro mol $\mathrm{C}$ ein mol $\mathrm{CO_2}$ produziert. Somit ergibt sich:
$$m_{\mathrm{CO_2}} = n_{\mathrm{C}} \cdot M_{\mathrm{CO_2}} \approx 2.15 \cdot 10^7 \, \mathrm{kg}$$
Also eine beträchtliche Menge, die jeden Tag durch den Betrieb des Kernkraftwerks eingespart wird!
i) Aus den Halbwertszeiten erhalten wir die Zerfallskonstanten:
$$k_{\mathrm{U}} = \frac{\ln(2)}{t_{1/2}(\mathrm{U})} \approx 1.5 \cdot 10^{-10} \, \mathrm{a^{-1}} \approx 4.9 \cdot 10^{-18} \, \mathrm{s^{-1}}$$
$$k_{\mathrm{Th}} = \frac{\ln(2)}{t_{1/2}(\mathrm{Th})} \approx 5.0 \cdot 10^{-11} \, \mathrm{a^{-1}} \approx 1.6 \cdot 10^{-18} \, \mathrm{s^{-1}}$$
Dann benötigen wir die Anzahl Atome der radioaktiven Stoffe in der Kohle:
$$N_{\mathrm{U}} = 1 \cdot 10^{-6} \cdot 4.89 \cdot 10^8 \mathrm{mol} \cdot 6.022 \cdot 10^{23} \mathrm{Atome/mol} \approx 2.9 \cdot 10^{26} \, \mathrm{Atome}$$
$$N_{\mathrm{Th}} = 2 \cdot 10^{-6} \cdot 4.89 \cdot 10^8 \mathrm{mol} \cdot 6.022 \cdot 10^{23} \mathrm{Atome/mol}\approx 5.8 \cdot 10^{26} \, \mathrm{Atome}$$
Die Aktivität ist dann:
$$A_{\mathrm{U}} = k_{\mathrm{U}} N_{\mathrm{U}} \approx 1.4 \cdot 10^{9} \, \mathrm{Bq}$$
$$A_{\mathrm{Th}} = k_{\mathrm{Th}} N_{\mathrm{Th}} \approx 9.1 \cdot 10^{8} \, \mathrm{Bq}$$
Schlussendlich ergibt sich die Aktivität durch Addition der Aktivitäten der beiden radioaktiven Stoffe:
$$A_{ges} = A_{\mathrm{U}} + A_{\mathrm{Th}} \approx 2.3 \cdot 10^{9} \, \mathrm{Bq}$$
j) Vorher war die Konzentration extrem niedrig, es waren ja nur $1$ bis $2$ Atome pro Million Atome Kohle. Nun ist die Konzentration extrem hoch, da die Kohlenstoffatome in $\mathrm{CO_2}$ in die Atmosphäre entwichen sind und nur die Verunreinigungen zurückbleiben.
$$D_{uran} = 1.53 \cdot 10^{-12} \, \frac{\mathrm{mSv/h}}{\mathrm{Bq/cm^3}} \frac{A}{V}$$
$$D_{thorium} = 2.06 \cdot 10^{-11} \, \frac{\mathrm{mSv/h}}{\mathrm{Bq/cm^3}} \frac{A}{V}$$
berechnet werden und verhält sich additiv. Dabei ist $A/V$ die Konzentration des jeweiligen Stoffes.
k) Nehme an, dass die radioaktiven Stoffe in der Asche zu $100\%$ (sinnvoll, da Gleichgewichtszustand) in eine Umgebung von $1\, \mathrm{km^3}$ freigesetzt werden. Berechne die zusätzliche Strahlenbelastung in $\mathrm{mSv/a}$ für die Umgebung. Das Kernkraftwerk Leibstadt verursacht nach eigenen Angaben eine Strahlenbelastung von maximal $0.01\, \mathrm{mSv/a}$ und produziert ähnlich viel Strom wie das oben betrachtete Kernkraftwerk Gösgen-Däniken [^6]. Verursacht also ein Kernkraftwerk oder ein Kohlekraftwerk mehr Strahlenbelastung?
Wir können direkt die gegebenen Formeln verwenden:
$$D_{\mathrm{U}} = 1.53 \cdot 10^{-12} \frac{\mathrm{mSv/h}}{\mathrm{Bq/cm^3}} \frac{1.4 \cdot 10^9 \, \mathrm{Bq}}{1 \, \mathrm{km^3}} \approx 1.9 \cdot 10^{-14} \, \mathrm{mSv/h}$$
$$D_{\mathrm{Th}} = 2.06 \cdot 10^{-11} \frac{\mathrm{mSv/h}}{\mathrm{Bq/cm^3}} \frac{9.1 \cdot 10^8 \, \mathrm{Bq}}{1 \, \mathrm{km^3}} \approx 1.7 \cdot 10^{-13} \, \mathrm{mSv/h}$$
Zusammen ergibt das:
$$D_{\mathrm{ges}} = D_{\mathrm{U}} + D_{\mathrm{Th}} \approx 1.9 \cdot 10^{-5} \, \mathrm{mSv/a}$$
Das ist deutlich weniger als die Strahlenbelastung durch das Kernkraftwerk Leibstadt. Somit verursacht ein Kernkraftwerk mehr Strahlenbelastung als ein Kohlekraftwerk, jedoch haben wir noch viele andere Schadstoffe nicht berücksichtigt, die durch den Betrieb eines Kohlekraftwerks in die Umwelt gelangen.
Quellen
[^1] KKW Gösgen-Däniken Stromproduktion
[^2] KKW Gösgen-Däniken Uranverbrauch
[^3] Wirkungsgrad Kohlekraftwerke
Woche 7 - Ableitungen, Integrale & Differentialgleichungen
Theorie
Ableitungen
Die Ableitung einer Funktion $f(x)$ an der Stelle $x_0$ ist definiert als
$$ f'(x_0) = \dd{f}{x} = \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} $$
Die Funktion $f'(x)$ gibt also die lokale Steigung der Funktion $f(x)$ an jeder Stelle $x$ an. Nun können wir fortfahren und uns fragen, was denn die Steigung von $f'(x)$ ist. Diese wird durch die zweite Ableitung $f''(x)$ beschrieben. Die zweite Ableitung ist also die Steigung der Steigung von $f(x)$.
Ableitungsregeln
In dieser Vorlesung sind wir an der Anwendung der Ableitung interessiert, die Definition ist für uns nicht so wichtig. Wir werden uns also v.a. mit den Ableitungsregeln beschäftigen, um gut damit rechnen zu können. Die wichtigsten sind (für $a, n, \delta$ und $c$ beliebige Konstanten (Zahlen)):
$$\text{Ableitung einer Konstanten: } \dd{}{x} c = 0$$
$$\text{Ableitung eines Polynoms: } \dd{}{x} (ax^n) = nax^{n-1}$$
$$\text{Ableitung der Exponentialfunktion: } \dd{}{x} \exp(ax) = a\exp(ax)$$
$$\text{Ableitung der Sinusfunktion: } \dd{}{x} \sin{(ax + \delta)} = a\cos{(ax + \delta)}$$
$$\text{Ableitung der Cosinusfunktion: } \dd{}{x} \cos{(ax + \delta)} = -a\sin{(ax + \delta)}$$
$$\text{Ableitung der Logarithmusfunktion: } \dd{}{x} \ln{(ax + \delta)} = \frac{1}{ax + \delta}$$
Die Ableitung ist eine linear. Das bedeutet, dass die Ableitung einer Summe von Funktionen gleich der Summe der Ableitungen der Summanden ist. Mit dem Produkt zweier Funktionen ist das nicht so einfach; aber damit befassen wir uns nächstes mal.
Integrale
Die Umkehrung der Ableitung wird als Integral bezeichnet. Das Integral einer Funktion $f(x)$ von $a$ bis $b$ ist definiert als
$$ \int_a^b f(x) \mathrm{d}x = \lim_{n \to \infty} \sum_{i=1}^n f(x_i) \Delta x_i $$
wobei $\Delta x_i = \frac{b-a}{n}$ und $x_i = a + i \Delta x_i$.
Als Umkehrung der Ableitung ist auch die Integration linear. Das bedeutet, dass das Integral einer Summe von Funktionen gleich der Summe der Integrale der Summanden ist.
Integrationsregeln
Diese Definition ist nicht wichtig für uns, wir werden uns v.a. mit den Regeln für das Integrieren beschäftigen. Die wichtigsten sind (für $a$ und $c$ beliebige Konstanten (Zahlen) und $n \neq -1$):
$$\text{Integral einer Konstanten: } \int c \mathrm{d}x = cx + C$$
$$\text{Integral eines Polynoms: } \int ax^n \mathrm{d}x = \frac{1}{n+1}ax^{n+1} + C$$
$$\text{Spezialfall: } \int \frac{1}{x} \mathrm{d}x = \ln{|x|} + C$$
$$\text{Integral der Exponentialfunktion: } \int \exp(ax) \mathrm{d}x = \frac{1}{a}\exp(ax) + C$$
$$\text{Integral der Sinusfunktion: } \int \sin{(ax + \delta)} \mathrm{d}x = -\frac{1}{a}\cos{(ax + \delta)} + C$$
$$\text{Integral der Cosinusfunktion: } \int \cos{(ax + \delta)} \mathrm{d}x = \frac{1}{a}\sin{(ax + \delta)} + C$$
wobei $C$ eine beliebige Konstante ist, denn diese fällt beim Ableiten ja weg.
Differentialgleichungen
Differentialgleichungen sind Gleichungen, in denen die gesuchte Variable nicht mehr einfach eine Zahl ist, sondern wir möchten eine Funktion finden, welche die Gleichungen für alle Werte der unabhängigen Variablen (bei $f(x)$ wird $x$ die unabhängige Variable genannt). Ein Beispiel für eine (einfache) Differentialgleichung ist
$$ \dd{f}{x} = f $$
Die Lösung dieser DGL erkennen wir gleich anhand der Ableitungsregel für die Exponentialfunktion:
$$ \dd{}{x} \exp(x) = \exp(x) $$
Die Lösung ist also $f(x) = \exp(x)$. In dieser Vorlesung müsst ihr grundsätzlich nicht selbst Differentialgleichungen lösen. Jedoch solltet ihr in der Lage sein zu überprüfen, ob ein gegebener Ansatz eine Differentialgleichung erfüllt oder nicht.
Aufgaben
Einfache Ableitungen
Hier ein paar einfache Ableitungen um ein Gefühl dafür zu bekommen. Damit ihr gleich abchecken könnt, ob eure Lösung stimmt, sind diese bereits freigeschaltet. Berechne die Ableitung der folgenden Funktionen:
$$f(x) = 3x^2$$
$$g(x) = 2x^3 + 3x^2$$
$$h(x) = 2x^3 + 3x^2 + 4x + 5$$
$$i(x) = \sin(x) + \cos(2x)$$
$$j(x) = \exp(5x) + \sin(x) + \cos(2x)$$
$$k(x) = \exp(8x) + \sin(0.1 x) + \cos(2x) + 3x^2$$
Einfache Integrale
Das gleiche mit ein paar einfachen Integralen. Finde die Funktionen, deren Ableitung die folgenden Funktionen sind:
$$l'(x) = 6x$$
$$m'(x) = 5x^2 + 2x^4$$
$$n'(x) = \exp(x) + \cos(2x)$$
$$o'(x) = \sin(x) + 22x^{22}$$
$$p'(x) = \exp(5x) + \sin(x) + \cos(2x)$$
Einfache Differentialgleichungen
Hier ein paar einfache Differentialgleichungen. Finde für jede die Lösung:
$$\dd{f}{x} = 5 f(x)$$
$$\dd{f}{x} = -2 f(x) + 3$$
$$\dd{^2 f}{x^2} = -f(x)$$
Dies ist etwa das Level, auf dem in dieser Vorlesung Differentialgleichungen lösen könnt. Es geht hier eher darum gegebene Ansätze zu überprüfen. Dies erfordert etwas Übung, aber grundsätzlich müsst ihr nur die Ableitungsregeln anwenden und einsetzen. Wir kennen jedoch noch nicht genügend Ableitungsregeln, um alle Differentialgleichungen lösen zu können. Das kommt nächstes mal.
Lösungen
Lösungen einfache Ableitungen
$$f'(x) = 6x$$
$$g'(x) = 6x^2 + 6x$$
$$h'(x) = 6x^2 + 6x + 4$$
$$i'(x) = \cos(x) - 2\sin(2x)$$
$$j'(x) = 5\exp(5x) + \cos(x) - 2\sin(2x)$$
$$k'(x) = 8\exp(8x) + 0.1\cos(0.1 x) - 2\sin(2x) + 6x$$
Lösungen einfache Integrale
$$l(x) = 3x^2 + C$$
$$m(x) = \frac{5}{3}x^3 + \frac{2}{5}x^5 + C$$
$$n(x) = \exp(x) + \frac{1}{2}\sin(2x) + C$$
$$o(x) = -\cos(x) + \frac{22}{23}x^{23} + C$$
$$p(x) = \frac{1}{5}\exp(5x) - \cos(x) + \frac{1}{2}\sin(2x) + C$$
Lösungen einfache Differentialgleichungen
Für $A, B$ beliebige Konstanten:
$$f(x) = A \exp(5x)$$
$$f(x) = A \exp(-2x) + 1.5$$
$$f(x) = A \sin(x) + B cos(x)$$
Woche 8 - Partielle Ableitungen, Wellengleichung & Linienspektren
Theorie
Repetition Ableitungsregeln
Letzte Woche haben wir uns die einfachen Ableitungsregeln angeschaut. Hier nochmal zur Erinnerung (für $a, n$ und $c$ beliebige Konstanten (Zahlen)):
$$\text{Ableitung einer Konstanten: } \dd{}{x} c = 0$$
$$\text{Ableitung eines Polynoms: } \dd{}{x} (ax^n) = nax^{n-1}$$
$$\text{Ableitung der Exponentialfunktion: } \dd{}{x} \exp(ax) = a\exp(ax)$$
$$\text{Ableitung der Sinusfunktion: } \dd{}{x} \sin{(ax + \delta)} = a\cos{(ax + \delta)}$$
$$\text{Ableitung der Cosinusfunktion: } \dd{}{x} \cos{(ax + \delta)} = -a\sin{(ax + \delta)}$$
$$\text{Ableitung der Logarithmusfunktion: } \dd{}{x} \ln{(ax + \delta)} = \frac{1}{ax + \delta}$$
Heute schauen wir uns an, wie sich die Ableitung von Verketteten und Multiplizierten Funktionen berechnen lässt.
Ableitung von Produkten von Funktionen
Betrachten wir das Produkt zweier Funktionen $f(x) = g(x) \cdot h(x)$, benötigen wir die Produktregel:
$$ \dd{f}{x} = \dd{g}{x} h + g \dd{h}{x} $$
Betrachten wir $f(x) = x^2 \cdot x^4$ als einfaches Beispiel um zu sehen, dass sie konsistent mit der Ableitung von Polynomen ist:
$$ \dd{f}{x} = \dd{x^2}{x} x^4 + x^2 \dd{x^4}{x} = 2x \cdot x^4 + x^2 \cdot 4x^3 = 2x^5 + 4x^5 = 6x^5 $$
Das gleiche Ergebnis erhalten wir, wenn wir zuerst die Funktion ausrechnen zu $f(x) = x^2 \cdot x^4 = x^6$ und dann die Ableitung davon bilden zu $\dd{f}{x} = 6x^5$.
Damit ihr jetzt nicht denkt, dass die Regel überflüssig ist noch ein Beispiel bei der sie auch wirklich benötigt wird:
$$ f(x) = \sin{(x)} \cdot \cos{(x)} $$
Hier ist $g(x) = \sin{(x)}$ und $h(x) = \cos{(x)}$. Die Ableitung ist:
$$ \dd{f}{x} = \dd{g}{x} h + g \dd{h}{x} = \cos{(x)} \cdot \cos{(x)} + \sin{(x)} \cdot (-\sin{(x)}) = \cos^2{(x)} - \sin^2{(x)} $$
Verkettete Funktionen
Eine verkettete Funktion ist eine Funktion, die aus mehreren Funktionen zusammengesetzt ist und wird beschrieben als $f(g(x))$. Die Regel besagt dann, dass die Ableitung gegeben ist durch:
$$ \dd{f}{x} = \dd{f}{g} \dd{g}{x} $$
Betrachten wir auch hier mit $f(x) = \exp{(5x)}$ ein Beispiel, das wir schon kennen um zu sehen, dass die Regel konsistent ist mit den bisher angewandten Regeln. Hier ist $f(g) = \exp(g)$ und $g(x) = 5x$. Die Ableitung ist:
$$ \dd{f}{x} = \dd{f}{g} \dd{g}{x} = \exp(g(x)) \cdot 5 = 5 \exp{(5x)} $$
Betrachten wir ein etwas schwierigeres Beispiel:
$$ f(x) = \sin{(x^2 + 1)} $$
Mit der Notation $f(g(x))$ ist $f(g) = \sin(g)$ und $g(x) = x^2 + 1$. Die Ableitung davon ist:
$$ \dd{f}{x} = \dd{f}{g} \dd{g}{x} = \cos{(x^2 + 1)} \cdot 2x $$
Diese Regel kann auch auf Verkettungen von mehr als zwei Funktionen angewendet werden. Betrachten wir zum Beispiel
$$ f(x) = \sin{(\exp{(x^2 + 1)})} $$
Mit der Notation $f(g(h(x)))$ ist $f(g) = \sin(g)$ und $g(h) = \exp(h)$ und $h(x) = x^2 + 1$. Die Ableitung davon ist:
$$ \dd{f}{x} = \dd{f}{g} \dd{g}{h} \dd{h}{x} = \cos{(\exp{(x^2 + 1)})} \cdot \exp{(x^2 + 1)} \cdot 2x $$
Die angewandte Regel nennt sich Kettenregel und ihr werdet sie in Analysis noch genauer kennenlernen. Hier müsst ihr sie einfach anwenden können.
Partielle Ableitungen
Letzte Woche haben wir uns die Ableitung für Funktionen mit lediglich einer unabhängigen Variablen angeschaut. In der Physik/physikalischen Chemie haben wir es aber oft mit Funktionen zu tun, welche von mehreren Variablen abhängen. Betrachten wir zum Beispiel ein Potential $V$ im dreidimensionalen Raum, so ist es eine Funktion der drei Ortsvariablen $x, y$ und $z$:
$$ V = V(x, y, z) $$
Wir können uns nun Fragen, was denn die Steigung der Funktion an einem spezifischen Punkt $(x_0, y_0, z_0)$ ist. Die Steigung ist definiert als die Änderung der Funktion pro Änderung der unabhängigen Variablen. Da wir hier mehrere unabhängige Variablen haben, müssen wir uns entscheiden, welche wir ändern wollen. Wir können zum Beispiel die Steigung in $x$-Richtung berechnen, indem wir die Funktion an der Stelle $(x_0 + \Delta x, y_0, z_0)$ auswerten und dann die Änderung durch $\Delta x$ teilen:
$$ \text{Steigung in } x \text{-Richtung: } \frac{V(x_0 + \Delta x, y_0, z_0) - V(x_0, y_0, z_0)}{\Delta x} $$
Dies ist aber gerade die Definition der Ableitung, wenn wir $\Delta x$ gegen Null gehen lassen und $y, z$ als Konstanten betrachten. Dies wird partielle Ableitung nach $x$ genannt und geschrieben als:
$$ \frac{\partial V}{\partial x} $$
Analog erhalten wir die partiellen Ableitungen nach $y$ und $z$, indem wir die anderen beiden Variablen als konstant annehmen und die Funktion nach $y$ bzw. $z$ ableiten:
$$ \frac{\partial V}{\partial y} \text{ und } \frac{\partial V}{\partial z} $$
Haben wir eine Differentialgleichung, mit Funktionen in mehreren Variablen, in der die partielle Ableitung vorkommt, so nennt man diese partielle Differentialgleichung. Ihr müsst diese nicht lösen können, solltet aber in der Lage sein zu überprüfen, ob eine gegebene Funktion sie erfüllt.
Die Wellengleichung
Die Wellengleichung ist eine partielle Differentialgleichung, welche die Ausbreitung von Wellen beschreibt. Sie lautet:
$$ \frac{\partial^2 \psi}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2} $$
Hier ist $\psi$ die Wellenfunktion, $x$ die Ortsvariable und $t$ die Zeitvariable. $v$ ist die Ausbreitungsgeschwindigkeit der Welle, z.B. für Licht die Lichtgeschwindigkeit $c$. Die Wellengleichung ist eine der wichtigsten Gleichungen in der Physik und wird in der Quantenmechanik verwendet, um die Wellenfunktion von Teilchen zu beschreiben. Hier geht es erst einmal darum zu lernen wie mit ihr mathematisch umgegangen wird. Ihr werdet sie in den Übungen und in der Vorlesung noch genauer kennenlernen.
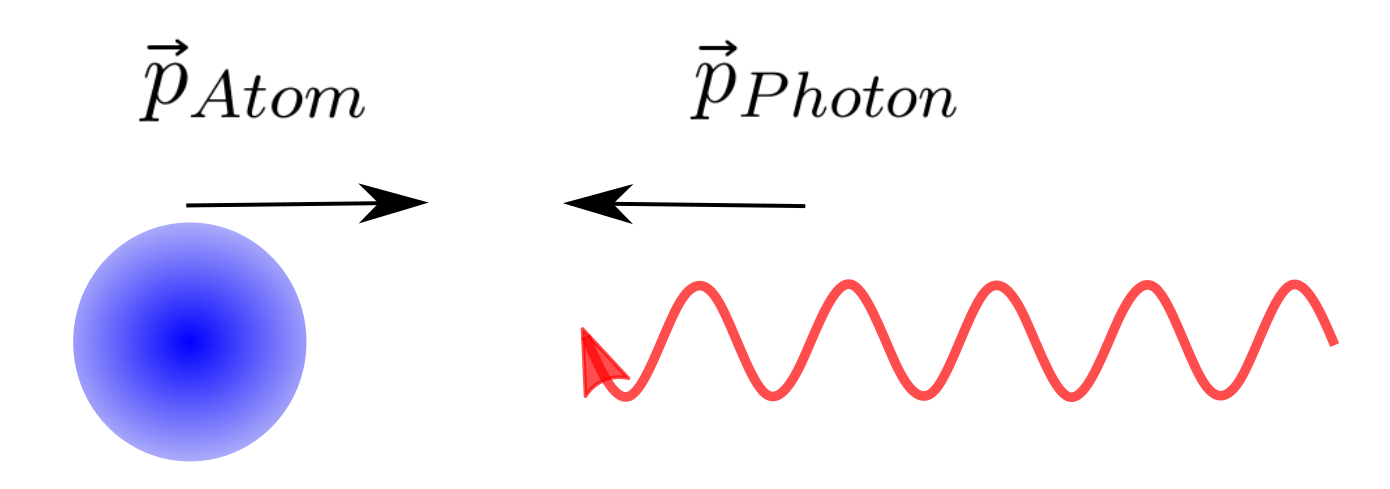
Photonen und deren Energie
Zur Einführung in die Quantenmechanik betrachten wir Licht, also elektromagnetische Wellen. Diese können als Teilchen betrachtet werden, die Photonen. Die Energie eines Photons ist gegeben durch
$$ E = h \nu = h \frac{c}{\lambda} $$
wobei $h$ das Plancksche Wirkungsquantum, $\nu$ die Frequenz, $c$ die Lichtgeschwindigkeit und $\lambda$ die Wellenlänge ist. Hier haben wir auch die Relation zwischen Frequenz und Wellenlänge benutzt:
$$ \nu = \frac{c}{\lambda} $$
Spektroskopie und Linienspektren
In der Quantenmechanik können sich die Elektronen nur auf bestimmten Energieniveaus (=Schalen) in einem Atom aufhalten. Das Energieniveau/die Schale in dem sich ein Elektron befindet, kann gewechselt werden, wenn dem Elektron durch ein Photon Energie hinzugefügt wird. Wird also monochromatisches (nur eine Wellenlänge, kein Gemisch) Licht in $x\mathrm{-Richtung}$ durch ein mit Wasserstoff gefülltes Gefäss geschickt und in $y\mathrm{-Richtung}$ ein Detektor angebracht, so werden nur bestimmte Wellenlängen detektiert. Fürs bessere Verständnis noch eine Animation der Balmer-Serie (Übergänge im Wasserstoff-Atom, die im sichtbaren Bereich liegen):
Balmer-Serie: Absorption von sichtbarem Licht durch anregen eines Elektrons von der zweiten in die dritte (rot) oder vierte (cyan) Schale. Die anderen Wellenlängen werden nicht absorbiert und gehen einfach durch.
Allgemeiner haben wir für den Übergang vom Zustand $n_1$ zum Zustand $n_2$ im Wasserstoff-Atom die Formel:
$$ E = h \nu = h c R_H \cdot \mathrm{abs}\bigg( \frac{1}{n_1^2} - \frac{1}{n_2^2} \bigg) $$
Aus dieser Formel können wir erkennen:
$$ \dd{}{n} \bigg( \frac{1}{n^2} \bigg) = - \frac{2}{n^3} $$
Die Energieniveaus liegen also immer näher beieinander! Ausserdem folgt aus $n \in \mathbb{N}$, dass es eine maximale Energie gibt, die freigesetzt werden kann, wenn ein Elektron aufgenommen wird. Diese Energie wird Ionisierungsenergie genannt. Wenn einem Elektron die Ionisierungsenergie zugeführt wird, so wird es aus dem Atom herausgeschlagen. Die Ionisierungsenergie des Wasserstoff-Atoms ist $E_\mathrm{ion} = 13.6\mathrm{eV}.$
Aufgaben
Ableitungen
Bestimme die Ableitungen der folgenden Funktionen:
- $f(x) = 3x^2 + 2x + 1$
- $g(x) = \exp{(x^3)}$
- $h(x) = 2x^2 \sin{(x^5)}$
- $i(x) = \sin{(\exp{(3x+5)})}$
- $j(x) = 5x + \exp{(\sin{(x)})} \cos{(x)}$
Partielle Ableitungen
Bestimme die partiellen Ableitungen der folgenden Funktionen (nach $x$ und $y$):
- $f(x, y) = 3x^2 + 2xy + y^2$
- $g(x, y) = x \exp{(x^2+y^2)}$
- $h(x, y) = \sin{(x^2+y^2)} \log{(x^2)}$
Partielle Differentialgleichungen
Zeige, dass die folgenden Funktionen die Wellengleichung
$$ \frac{\partial^2 \psi}{\partial x^2} = \frac{1}{v^2} \frac{\partial^2 \psi}{\partial t^2} $$
nicht erfüllen:
- $\psi_1(x,t) = x^2 t$
- $\psi_2(x,t) = \sin{(x)} \cos{(t)}$
- $\psi_3(x,t) = x \sin{(x + vt)}$
Zeige, dass die folgende Funktion die Wellengleichung erfüllt:
$$ \psi_4(x,t) = A \sin{(x + vt)} + B \cos{(x+vt)} $$
Einheiten-Konvention
In der Spektroskopie ist es üblich die Energie in Wellenzahlen anzugeben. Dabei ist die Wellenzahl definiert als:
$$ \tilde{\nu} = \frac{1}{\lambda} $$
wobei $\lambda$ die Wellenlänge ist. Die Einheit der Wellenzahl ist $\mathrm{cm}^{-1}$. Die Umrechnung von Wellenzahl in Energie ist gegeben durch:
$$ E = h c \tilde{\nu} $$
wobei $h$ das Plancksche Wirkungsquantum und $c$ die Lichtgeschwindigkeit ist. Die Einheit der Energie ist $\mathrm{J}$.
- Berechne die zur Wellenzahl $\tilde{\nu} = 1000\, \mathrm{cm}^{-1}$ gehörende Energie in $\mathrm{J}.$
- Berechne die zur Energie $E = 3\, \mathrm{eV}$ gehörende Wellenzahl in $\mathrm{cm}^{-1}.$
Spektroskopie Einführung
Betrachte den Übergang in einem Wasserstoff-Atom von der Schale $n=7$ zur Schale $n=2$.
- Wird dabei Energie freigesetzt oder aufgenommen?
- Welche Energie wird für diesen Übergang benötigt/freigesetzt?
- Welche Wellenlänge hat das emittierte/absorbierte Licht?
Spektroskopie fortgesetzt
Wir haben die Rydberg-Formel kennen gelernt, um die Energie von Übergängen im Wasserstoff-Atom zu berechnen. Diese lässt sich einfach verallgemeinern auf Wasserstoff ähnliche Atome (Atome mit nur einem Elektron, aber beliebiger Kernladungszahl) und lautet dann:
$$ E = h c Z^2 R_K \cdot \mathrm{abs}\bigg( \frac{1}{n_1^2} - \frac{1}{n_2^2} \bigg) $$
wobei $Z$ die Kernladungszahl ist und $R_K$ die Rydberg-Konstante. Für Wasserstoff ist $Z=1$ und $R_K = R_H$. Für einen Atomkern der Masse $m_K$ und einem Elektron der Masse $m_e$ ist die Rydberg-Konstante gegeben durch:
$$ R_K = \frac{m_K}{m_K + m_e} R_{\infty} $$
- Berechne die Rydberg-Konstante für das $^{23}\mathrm{Na}^{10+}$-Ion.
- Berechne die Energie des Übergangs $n_1 = 3 \rightarrow n_2 = 2$ im $^{23}\mathrm{Na}^{10+}$-Ion.
- Berechne die Wellenlänge des emittierten/absorbierten Lichts für den Übergang in 2.
- Was ist die Ionisierungsenergie des $^{23}\mathrm{Na}^{10+}$-Ions?
- Wir betrachten zwei aufeinanderfolgende Übergänge im $^{23}\mathrm{Na}^{10+}$-Ion, von $n_i$ nach $n_f$ und von $n_i$ nach $n_f + 1.$. Die Energien der Übergänge sind $E_{n_i \rightarrow n_f} = 123.4\mathrm{eV}$ und $E_{n_i \rightarrow n_f + 1} = 129.9\mathrm{eV}$. Bestimme $n_i \text{ und } n_f.$
Hinweis: Benutze zur Vereinfachung die Formel
$$ \frac{1}{n^2} - \frac{1}{(n+1)^2} \approx \frac{2}{(n+\frac{1}{2})^{3}} $$
Lösungen
Lösung Ableitungen
- $f'(x) = 6x + 2$
- $g'(x) = 3x^2 \exp{(x^3)}$
- $h'(x) = 4x \sin{(x^5)} + 10x^6 \cos{(x^5)}$
- $i'(x) = 3 \exp{(3x+5)} \cos{(\exp{(3x+5)})}$
- $j'(x) = 5 - \exp{(\sin{(x)})} \sin{(x)} + \exp{(\sin{(x)})} \cos{(x)} \cos{(x)}$
Lösung partielle Ableitungen
- $\frac{\partial f}{\partial x} = 6x + 2y$ und $\frac{\partial f}{\partial y} = 2x + 2y$, $\frac{\partial f}{\partial y} = 2x + 2y$
- $\frac{\partial g}{\partial x} = \exp{(x^2+y^2)} + 2x^2 \exp{(x^2+y^2)}$ und $\frac{\partial g}{\partial y} = 2xy \exp{(x^2+y^2)}$
- $\frac{\partial h}{\partial x} = 2x \cos{(x^2+y^2)} \log{(x^2)} + \frac{2x}{\partial x^2}$ und $\frac{\partial h}{\partial y} = 2y \cos{(x^2+y^2)} \log{(x^2)}$
Lösung partielle Differentialgleichungen
- $\frac{\partial^2 \psi_1}{\partial x^2 t} = 2 t$ und $\frac{\partial^2 \psi_1}{\partial t^2} = 0$ was nicht gleich sein kann.
- $\frac{\partial^2 \psi_2}{\partial x^2} = -\sin{(x)} \cos{(t)}$ und $\frac{\partial^2 \psi_2}{\partial t^2} = -\sin{(x)} \cos{(t)}$ was gleich ist, aber der Faktor $1/v^2$ fehlt.
- $\frac{\partial^2 \psi_3}{\partial x^2} = 2 \cos{(x+vt)} - x \sin{(x+vt)}$ und $\frac{\partial^2 \psi_3}{\partial t^2} = -v^2 \sin{(x + vt)}$ was z.B. für $x = -vt$ nicht gleich sein kann (rechte Seite ist $0$, linke Seite ist $2$).
Die partiellen Ableitungen von $\psi_4(x,t)$ sind:
$$ \begin{aligned} \frac{\partial^2 \psi_4}{\partial x^2} &= -A \sin{(x + vt)} - B \cos{(x+vt)} \\ \frac{\partial^2 \psi_4}{\partial t^2} &= -A v^2 \sin{(x + vt)} - B v^2 \cos{(x + vt)} \end{aligned}$$
womit wir genau das erforderte Verhältnis von $1/v^2$ erhalten.
Lösung Einheiten-Konvention
- $E \approx 1.986 \cdot 10^{-20}\, \mathrm{J}$
- $\tilde{\nu} \approx 2.4 \cdot 10^4\, \mathrm{cm}^{-1}$
Lösung Spektroskopie Einführung
- Es wird Energie freigesetzt, da $n_1 > n_2$, das Elektron also ein energieärmeres Niveau einnimmt.
- Wir wenden die Rydberg-Formel an:
$$ \begin{aligned}E &= h c R_H \cdot \mathrm{abs}\bigg( \frac{1}{n_1^2} - \frac{1}{n_2^2} \bigg) \\ &= 13.6\mathrm{eV} \cdot \mathrm{abs}\bigg( \frac{1}{7^2} - \frac{1}{2^2} \bigg) \approx 3.12\, \mathrm{eV} \end{aligned} $$
- Mit $E = \frac{h c}{\lambda}$ erhalten wir $\lambda = \frac{h c}{E} \approx 397\, \mathrm{nm}$
Lösung Spektroskopie fortgesetzt
- $ R_{Na} = \frac{m_{Na}}{m_{Na} + m_e} R_{\infty} \approx 1.097 \cdot 10^5\, \mathrm{cm}^{-1} $
- Beim Übergang $n_1 = 3 \rightarrow n_2 = 2$ wird Energie freigesetzt. Wir berechnen die Energie mit der Rydberg-Formel:
$$ \Delta E = h c Z^2 R_{Na} \cdot \mathrm{abs}\bigg( \frac{1}{3^2} - \frac{1}{2^2} \bigg) \approx 189\, \mathrm{eV} $$
- $\lambda = \frac{h c}{\Delta E} \approx 656\, \mathrm{nm}$
- Die Ionisierungsenergie ist die für den Übergang $n_1 = 1 \rightarrow n_2 = \infty$ benötigte Energie. Wir erkennen aus der Rydberg-Formel, dass diese Energie $R_{Na} \approx 1.097 \cdot 10^5\, \mathrm{cm}^{-1} \equiv 1360.5\, \mathrm{eV}$ beträgt.
- Da wir die Energien der beiden Übergänge kennen, können wir die Rydberg-Formel anwenden und erhalten:
$$ E_1 = h c R_{Na} \cdot \mathrm{abs}\bigg( \frac{1}{n_i^2} - \frac{1}{(n_f)^2} \bigg) $$ $$ E_2 = h c R_{Na} \cdot \mathrm{abs}\bigg( \frac{1}{n_i^2} - \frac{1}{(n_f+1)^2} \bigg) $$
Wir können die beiden Gleichungen voneinander subtrahieren und erhalten
$$ E_1 - E_2 = h c R_{Na} \cdot \mathrm{abs}\bigg( \frac{1}{n_f^2} - \frac{1}{(n_f+1)^2} \bigg) $$
und mit der Formel aus dem Hinweis
$$ \frac{1}{n^2} - \frac{1}{(n+1)^2} \approx \frac{2}{(n+\frac{1}{2})^{3}} $$
ergibt sich
$$ E_1 - E_2 = h c Z^2 R_{Na} \cdot \frac{2}{(n_f+\frac{1}{2})^{3}} $$
Womit wir $n_f$ bestimmen können:
$$ n_f = \sqrt[3]{\frac{2 h c Z^2 R_{Na}}{E_1 - E_2}} - \frac{1}{2} \approx 6.98 \approx 7 $$
und unter einer weiteren Verwendung der Rydberg-Formel
$$ n_i = \sqrt{\frac{1}{\mathrm{abs}\bigg( \frac{E}{h c Z^2 R_{Na}} - \frac{1}{n_f^2} \bigg)}} \approx 3.01 \approx 3 $$
Woche 9 - Photoelektrischer Effekt & Bohr-Modell
Theorie
Reduzierte Masse
Betrachten wir zwei Teilchen der Massen $m_1$ und $m_2$, die sich frei bewegen können, so können die Bewegungsgleichungen in die Bewegung des Schwerpunktes und die Relativbewegung der beiden Teilchen aufgeteilt werden. Oft spielt aber nur die Relativbewegung eine Rolle, und wir wählen ein Koordinatensystem, das sich mit dem Schwerpunkt mitbewegt. So haben wir unser Zweikörperproblem auf ein Einkörperproblem reduziert. Das leichtere Teilchen verhält sich dabei wie ein Teilchen mit der reduzierten Masse $\mu$:
$$\mu = \frac{m_1 m_2}{m_1 + m_2}$$
Keine Angst, ihr müsst das nicht herleiten. Aber das Konzept wird beim Lösen der Schrödingergleichung verwendet und nur sehr kurz erklärt in der Vorlesung.
Photoelektrischer Effekt
Beim photoelektrischen Effekt wird Licht auf eine Metalloberfläche geschossen. Dabei werden Elektronen aus dem Metall herausgeschlagen. Die Energie der Elektronen hängt dabei von der Frequenz des Lichts ab, nicht aber von der Intensität. Dies ist ein weiterer Nachweis für die Quantisierung der Energie.
Wird ein Elektron aus einem Metall herausgeschlagen, so muss dafür eine gewisse Energie aufgewendet werden, das Metall gibt ja seine Elektronen nicht freiwillig ab. Diese Energie wird Austrittsarbeit genannt. Was dann noch übrig bleibt ist die kinetische Energie des herausfliegenden Elektrons.
Bohrsches Atommodell
Das Bohrsche Atommodell beschreibt das Atom als ein System aus einem positiv geladenen Atomkern und einer negativ geladenen Elektronenhülle. Die Elektronen bewegen sich auf Kreisbahnen um den Atomkern. Hier wird aber eine künstliche Quantisierung eingeführt: Es sind nur bestimmte Kreisbahnen möglich, gerade diese mit dem Bahndrehimpuls $L = n \hbar$. Dabei kann $n$ eine beliebige natürliche Zahl sein und wird als Hauptquantenzahl bezeichnet. Die Bahnen werden auch als Schalen bezeichnet. Da sich die Elektronen nur auf diesen Schalen aufhalten können und nicht dazwischen (und wie in der letzten Übung gesehen die Energie von der Schale abhängt), ist die Energie der Elektronen quantisiert.
Wellen-Teilchen Dualismus
In der Quantenmechanik beschreiben wir physikalische Systeme nicht mehr durch Teilchen und deren Positionen, sondern durch Wellenfunktionen. Daher können wir 'klassisch betrachtete' Teilchen auch als Welle interpretieren, welche die de-Broglie-Wellenlänge hat:
$$\lambda = \frac{h}{p}$$
wobei $p$ der Impuls des Teilchens ist.
Aufgaben
Photoelektrischer Effekt
- Betrachte einen Laser, der Licht mit einer Wellenlänge von $\lambda = 200\, \mathrm{nm}$ aussendet. Wie gross ist die Energie eines einzelnen Photons? (in $\mathrm{eV}$)
- Wir betrachten eine Kupferplatte, deren Austrittsarbeit $W_A = 4.7\, \mathrm{eV}$ beträgt. Wie gross ist die maximale kinetische Energie der Elektronen, die aus dem Metall herausgeschlagen werden können, wenn Licht mit einer Wellenlänge von $\lambda = 200\, \mathrm{nm}$ (wie in 1.) auf die Platte geschossen wird?
Sonnensystem als Atommodell (schwierig)
Betrachte das Sonnensystem als Atommodell. Die Sonne ist der Atomkern, die Planeten sind die Elektronen. Die Bahnen der Planeten sind die Schalen.

WP, CC BY-SA 3.0, via Wikimedia Commons
- Welche Hauptquantenzahl $n$ würdest du der Erde geben?
- Die Erde hat eine Masse von $m_E \approx 6 \cdot 10^{24}\, \mathrm{kg}$ und die Sonne hat eine Masse von $m_S \approx 2 \cdot 10^{30}\, \mathrm{kg}$. Wie gross ist die Bahngeschwindigkeit der Erde? (Nehme an, dass sich die Erde auf einer Kreisbahn um die Sonne bewegt und vernachlässige den Einfluss der anderen Planeten).
- Berechne den Betrag vom Bahndrehimpuls der Bewegung der Erde um die Sonne.
- Formuliere eine Analogie der Bohrschen Postulate für das Sonnensystem.
- Angenommen die Erde hat die von dir in Aufgabe 1 bestimmte Hauptquantenzahl. Was für einen Bahndrehimpuls müsste demnach Neptun haben?
- Neptun hat eine Masse von $m_N \approx 1 \cdot 10^{26}\, \mathrm{kg}$. Wie lange dauert nach unserem Modell ein Jahr auf Neptun?
- In Wirklichkeit dauert ein Jahr für Neptun $T_N \approx 5 \cdot 10^9\, \mathrm{s}$. Bedeutet das, dass das Bohr-Modell nicht funktioniert?
Reduzierte Masse
Berechne die reduzierte Masse (schlage allenfalls die Definition nach) für die folgenden Systeme:
- $m_1 = 1\, \mathrm{u}$ und $m_2 = 1\, \mathrm{u}$
- $m_1 = 2\, \mathrm{u}$ und $m_2 = 2\, \mathrm{u}$
- $m_1 = 1\, \mathrm{u}$ und $m_2 = 1\, \mathrm{kg}$
- $m_1 = 1\, \mathrm{kg}$ und $m_2 = 1\, \mathrm{u}$
De-Broglie-Wellenlänge
- Berechne die de-Broglie-Wellenlänge von einem Auto ($m = 1000\, \mathrm{kg}$), das mit $v = 30\, \mathrm{m/s}$ fährt.
- Welches der folgenden Objekte hat die grösste de-Broglie Wellenlänge? i) Ein Helium Atom bei Raumtemperatur (Geschwindigkeit $v \approx 800\, \mathrm{m/s}$) ii) Eine Maus, die von einer Katze gejagt wird iii) Ein von Roger Federer geschlagener Tennisball
Lösungen
Lösung Photoelektrischer Effekt
- $E = \frac{h c}{\lambda} \approx 6.19\, \mathrm{eV}$
- $E_{kin} = E - W_A \approx 1.49\, \mathrm{eV}$
Lösung Sonnensystem als Atommodell
L1. Analog zum Bohrschen Atommodell fangen wir mit der Quantenzahl $n = 1$ für die innerste Schale an. Die Erde ist der dritte Planet von der Sonne aus, also $n = 3$. L2. Die Bedingung für eine Kreisbahn ist $F_G = F_Z$ (Gravitationskraft = Zentripetalkraft). Die Gravitationskraft ist gegeben durch $F_G = \frac{G m_S m_E}{r^2}$ und die Zentripetalkraft durch $F_Z = \frac{m_E v^2}{r}$. Setzen wir diese gleich, so erhalten wir:
$$\frac{G m_S m_E}{r^2} = \frac{m_E v^2}{r} \Rightarrow \frac{G m_S}{r} = v^2 \qquad (1)$$
Wir erinnern uns daran, dass ein Jahr $365.25\, \mathrm{Tage}$ dauert und der Umlaufzeit $T$ der Erde um die Sonne entspricht. Die Umlaufbahn lässt sich berechnen durch $U = 2 \pi r = v T$. Nach $r$ aufgelöst erhalten wir:
$$r = \frac{v T}{2 \pi} \qquad (2)$$
Setzen wir nun (2) in (1) ein, so erhalten wir:
$$\frac{G m_S}{\frac{v T}{2 \pi}} = v^2 \Rightarrow v = \sqrt[3]{\frac{G m_S 2 \pi}{T}} \approx 3 \cdot 10^{4}\, \mathrm{m/s}$$
L3. Der Bahndrehimpuls ist gegeben durch $l_E = m_E v r$. Setzen wir (2) ein, so erhalten wir:
$$l_E = m_E v r = m_E v \frac{v T}{2 \pi} = \frac{m_E T}{2 \pi} v^2 \approx 3 \cdot 10^{40}\, \mathrm{kg m^2 s^{-1}}$$
L4. Format: Bohrsches Postulat -> Analogie
i) Die Elektronen bewegen sich auf diskreten Kreisbahnen um den Atomkern. -> Die Planeten bewegen sich auf diskreten Kreisbahnen um die Sonne.
ii) Die kreisförmige Bewegung erfolgt strahlungslos. Wird von aussen Strahlung zugeführt, so kann sie nur vom Atom absorbiert werden, wenn die Energie der Strahlung genau der Differenz der Energieniveaus entspricht. -> Die Bahnen der Planeten sind stabil und können nur verändert werden, wenn Asteroiden mit einer Energie auf die Planeten treffen, die genau der Differenz der Energieniveaus der Bahnen entspricht.
iii) Der Betrag des Drehimpulses eines gebundenen Elektrons nimmt nur die diskreten Werte $l_n = n \hbar$ an. -> Der Betrag des Drehimpulses eines Planeten im Sonnensystem nimmt nur die diskreten Werte $l_n = n k$ an, wobei die Konstante $k$ durch den Drehimpuls der Erde und der zugehörigen Hauptquantenzahl $n$ bestimmt ist. (Teilaufgaben 1. und 3.)
L5. Haben wir der Erde die Quantenzahl $n = 3$ gegeben, so ist die natürliche Wahl für die Quantenzahl von Neptun $n = 8$. Wenden wir Postulat iii) an und unser Ergebnis aus Aufgabe 3, so erhalten wir:
$$l_N = 8 k = 8 \frac{1}{3} l_E \approx 7 \cdot 10^{40}\, \mathrm{kg m^2 s^{-1}}$$
L6. Wir haben die Gleichungen für die Umlaufbahn:
$$U = 2 \pi r_N = v_N T \Rightarrow r_N = \frac{v_N T}{2 \pi} \qquad (1)$$
und für den Bahndrehimpuls:
$$l_N = m_N r_N v_N \qquad (2)$$
Ausserdem muss auch hier wieder die Bedingung für eine Kreisbahn erfüllt werden, also $F_G = F_Z$. Setzen wir diese beiden Gleichungen gleich, so erhalten wir:
$$\frac{G m_S m_N}{r_N^2} = \frac{m_N v_N^2}{r_N} \Rightarrow v_N^2 = \frac{G m_S}{r_N} \qquad (3)$$
Setzen wir (1) in (2) und (3) ein, so erhalten wir:
$$l_N = m_N \frac{v_N T}{2 \pi} v_N = \frac{m_N v_N^2 T}{2 \pi} \qquad (4)$$
$$v_N^2 = \frac{G m_S}{\frac{v_N T}{2 \pi}} \Rightarrow v_N = \sqrt[3]{\frac{2 \pi G m_S}{T}} \qquad (5)$$
Setzen wir (5) in (4) ein:
$$l_N = \frac{m_N \left(\frac{2 \pi G m_S}{T}\right)^{2/3} T}{2 \pi} = \frac{m_N \left(G m_S\right)^{2/3} T^{1/3}}{\left(2 \pi\right)^{1/3}}$$
und nach $T$ aufgelöst ergibt sich schlussendlich:
$$T = \frac{2 \pi l_N^3}{m_N^3 G^2 m_S^2} \approx 1 \cdot 10^5\, \mathrm{s}$$
L7. Nein, denn wir betrachten hier ein makroskopisches System! Die Annahme iii), dass dass der Drehimpuls der Planeten diskrete Werte annimmt, stimmt so nicht. Auf der hier betrachteten Grössenskala hätten wir ein kontinuierliches Spektrum von Drehimpulsen.
Lösung reduzierte Masse
- $\mu = \frac{1 \cdot 1}{1 + 1} \mathrm{u} = \frac{1}{2} \, \mathrm{u}$
- $\mu = \frac{2 \cdot 2}{2 + 2} \mathrm{u} = 1 \mathrm{u}$
- $\mu = \frac{1\, \mathrm{u} \cdot 1\, \mathrm{kg}}{1\, \mathrm{u} + 1\, \mathrm{kg}} \approx 1\, \mathrm{u}$
- Gleich wie 3., da die reduzierte Masse unabhängig von der Reihenfolge der Teilchen ist.
Lösung De-Broglie-Wellenlänge
- $\lambda = \frac{h}{p} = \frac{h}{m v} \approx 2.2 \cdot 10^{-38} \, \mathrm{m}$
- i) $\begin{aligned}m_{He} &\approx 4 \mathrm{u} \approx 7 \cdot 10^{-27} \mathrm{kg} \ & \Rightarrow \lambda = \frac{h}{m_{He} v_{He}} \approx 1.3 \cdot 10^{-10}\, \mathrm{m} \end{aligned}$ ii) $m \approx 0.1\, \mathrm{kg}, v \approx 2\, \mathrm{m/s} \Rightarrow \lambda \approx 3 \cdot 10^{-33}\, \mathrm{m}$ iii) $m \approx 0.05\, \mathrm{kg}, v \approx 60\, \mathrm{m/s} \Rightarrow \lambda \approx 2 \cdot 10^{-34}\, \mathrm{m}$ Also hat das Helium Atom ganz klar die grösste Wellenlänge. Das ist auch nicht überraschend, da alle anderen betrachteten Objekte makroskopisch sind und viel grössere Massen haben.
Woche 10 - Photonenimpuls & Interferenz
Theorie
Photonenimpuls
Letzte Woche haben wir die Wellenlänge von Materieteilchen betrachtet, die De-Broglie-Wellenlänge:
$$\lambda = \frac{h}{p}$$
Betrachten wir Teilchen als Materie, so kennen wir (meist) ihre Masse $m$ und ihre Geschwindigkeit $v$, womit sich der Impuls durch $p = m v$ ergibt. Betrachten wir Photonen als Teilchen, so kennen wir ihre Wellenlänge (oder können sie aus anderen Eigenschaften wie der Energie oder Frequenz berechnen) und erhalten den Impuls durch umstellen der De-Broglie-Wellenlänge:
$$p = \frac{h}{\lambda}$$
Wieso ist das wichtig? Nun, wir wissen aus der Physik, dass bei einem Zusammenstoss von Teilchen der Gesamt-Impuls erhalten bleibt. Wenn also ein Photon von einem Teilchen absorbiert wird, dann wird der Impuls auf das Teilchen übertragen und es wird (nur sehr leicht, da der Impuls eines Photons recht klein ist) beschleunigt in die Richtung, in die das Licht sich davor ausgebreitet hat. Genauso wird ein Teilchen, das ein Photon aussendet in die entgegengesetzte Richtung beschleunigt, gerade wie der Rückstoss beim abfeuern einer Kanonenkugel.
Interferenz
Überlagern sich zwei Wellen, so addieren sich die Amplituden der Wellen. Dies kann mathematisch so simpel beschrieben werden wie es klingt: Haben wir zwei Wellenfunktionen $A_1(x, t)$ und $A_2(x, t)$, so ergibt sich die resultierende Wellenfunktion $A(x, t)$ durch $A(x, t) = A_1(x, t) + A_2(x, t)$. Dies führt zu einem Phänomen, welches wir als Interferenz bezeichnen. Haben wir zwei Wellen, die sich überlagern, so können wir zwei Extremfälle unterscheiden:
- Die Wellen sind in Phase, d.h. die Maxima und Minima der Wellen fallen aufeinander. In diesem Fall verstärken sich die Wellen und wir erhalten eine resultierende Welle mit grösserer Amplitude. Dies passiert zum Beispiel für $A_1(x, t) = \cos(k x + v t)$ und $A_2(x, t) = 5 \cos(k x + v t)$ zu $A(x, t) = 6 \cos(k x + v t)$. Dieser Fall trifft auf, wenn die Phasendifferenz zweier Wellen ein ganzzahliges Vielfaches von $2 \pi \lambda$ beträgt.
- Die Wellen verlaufen gegenphasig, d.h. die Maxima der einen Welle fallen auf die Minima der anderen Welle. In diesem Fall löschen sich die Wellen aus und wir erhalten eine resultierende Welle mit kleinerer Amplitude. Dies passiert zum Beispiel für $A_1(x, t) = \cos(k x + v t)$ und $A_2(x, t) = -2 \cos(k x + v t)$ zu $A(x, t) = - \cos(k x + v t)$. Dieser Fall trifft auf, wenn die Phasendifferenz zweier Wellen ein ganzzahliges Vielfaches von $2 \pi \lambda$ beträgt.
Wir werden hier nur diese beiden Extremfälle und nur Wellen mit der gleichen Ausbreitungsgeschwindigkeit betrachten, denn sonst wird es schnell kompliziert, da die Amplitude der resultierenden Welle zeitabhängig wird. In der Übung beschäftigt ihr euch mit dem Doppelspaltexperiment, welches als Paradebeispiel für Interferenz gilt.
Etwas zum spielen:
Durch auswählen der Optionen kannst du Animationen von Wasser, Licht oder Schallwellen und deren Interferenz verhalten beobachten.
Aufgaben
Photonenimpuls (Konzeptfrage)
Angenommen die Sonne sendet pro Sekunde $10^{45}$ Photonen aus. Wie gross ist die resultierende Kraft, die auf die Sonne wirkt, wenn die Photonen mit einer Wellenlänge von $500\,\mathrm{nm}$ ausgesendet werden? Hinweis: Die Kraft ergibt sich durch $F = \frac{\Delta p}{\Delta t}$.
Photonenimpuls (Rechnen)
- Betrachte einen Laser, der violettes Licht mit einer Wellenlänge von $\lambda = 400\, \mathrm{nm}$ aussendet. Berechne die Energie und den Impuls eines Photons.
- Der Laser aus 1. sendet pro Sekunde $10^{20}\, \mathrm{Photonen}$ aus. Was ist die Leistung des Lasers? Wie viel Impuls wird pro Sekunde ausgesendet?
- Betrachte ein Papierflugzeug mit einer Masse von $m = 2\,\mathrm{g}$, das mit einer Geschwindigkeit von $v = 5\,\mathrm{m/s}$ fliegt. Wie gross ist der Impuls des Flugzeugs?
- Das Papierflugzeug sei aus schwarzem Papier und absorbiere alles auftreffende Licht (vorherige Teilaufgaben). Wie lange dauert es, bis es durch den Laser gestoppt wurde?
- Was passiert wahrscheinlich in der Realität, wenn wir dieses Experiment durchführen?
Interferenz
- Berechne die Superposition der Wellen $A_1(x) = \sin(x + \pi / 2)$ und $A_2(x, t) = 5 \cos(x)$.
- Betrachte zwei Laser mit der gleichen Wellenlänge $\lambda = 500\,\mathrm{nm}$, die in einem Abstand von $d = 4700\, \mathrm{nm}$ voneinander aufgestellt wurden. Wie gross muss die Phasendifferenz der beiden Laser sein, damit destruktive Interferenz beobachtet werden kann? Hinweis: Siehe Bild unten.
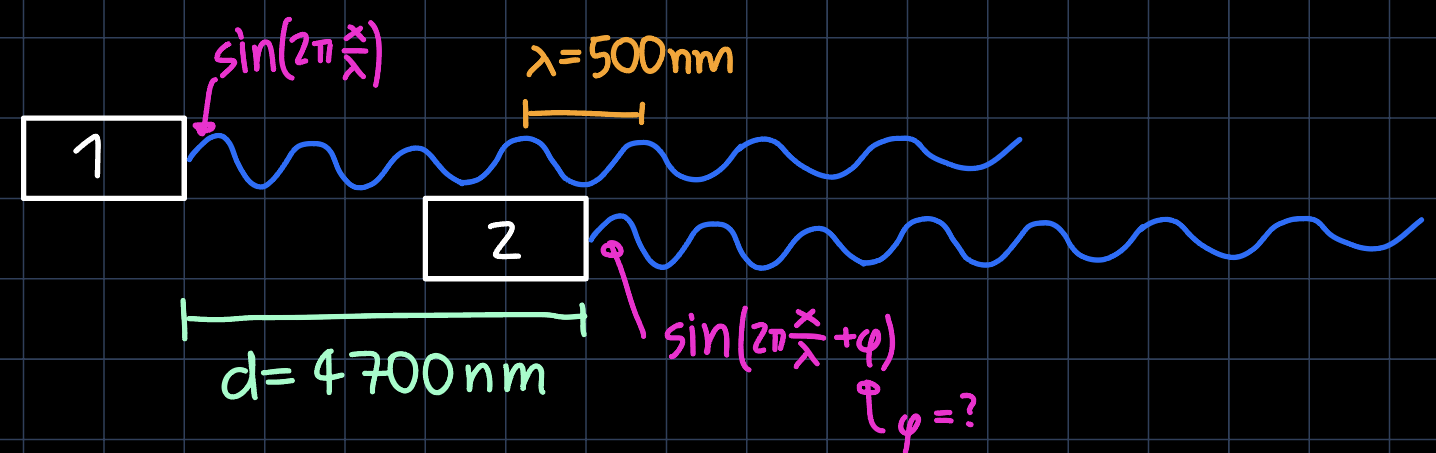
Lösungen
Lösung Photonenimpuls (Konzeptfrage)
Da die Photonen in alle Richtungen gleichermassen ausgesendet werden, verschwindet die resultierende Kraft. Die Kraft, die auf die Sonne wirkt, ist also $F_{res} = 0\,\mathrm{N}$.
Lösung Photonenimpuls (Rechnen)
- $E = h \nu = \frac{hc}{\lambda} \approx 4.96 \cdot 10^{-19}\,\mathrm{J}$, $p = \frac{h}{\lambda} \approx 1.66 \cdot 10^{-27}\,\mathrm{kg\,m/s}$
- Die Leistung ist definiert als Energie pro Zeit, also $P = \frac{N E}{t} \approx 49.6 \,\mathrm{W}$. Der Impuls ergibt sich gleichermassen durch $\frac{p_{laser}}{s} = \frac{N p}{t} \approx 1.66 \cdot 10^{-7}\,\mathrm{kg\,m/s^2}$.
- $p_{flugzeug} = m v = 0.01\,\mathrm{kg\,m/s}$
- Damit das Flugzeug gestoppt wird muss $p_{laser} = p_{flugzeug}$ gelten. Es dauert also $t = \frac{p_{flugzeug}}{p_{laser}/\mathrm{s}} \approx 6 \cdot 10^{4}\,\mathrm{s} \approx 17 \, \mathrm{h}$.
- Die Leistung des Lasers ist so gross, dass das Flugzeug relativ schnell verbrennen würde. Ausserdem müssten wir irgendwie verhindern, dass das Flugzeug durch Luftwiderstand abgebremst wird und nicht abstürzt aufgrund der Schwerkraft.
Lösung Interferenz
- $A(x) = \sin(x + \pi / 2) + 5 \cos(x) = \cos(x) + 5 \cos(x) = 6 \cos(x)$
- Damit die beiden Wellen ausser Phase sind, muss die resultierende Phasendifferenz $\pi$ betragen. Da der zweite Laser $d = 4700\, \mathrm{nm}$ vom ersten entfernt ist, können wir einfach $d$ auf das Argument addieren und erhalten $A_1(x) = \sin(2 \pi \frac{x}{\lambda})$ und $A_2(x) = \sin(2 \pi \frac{x+d}{\lambda}+\varphi)$. Damit die Summe verschwindet, muss $2 \pi \frac{x}{\lambda} + (2n + 1) \pi = 2 \pi \frac{x+d}{\lambda} + \varphi$, wobei $n \in \mathbb{Z}$ gelten. Damit folgt direkt $\varphi = 2 \pi \frac{d}{\lambda} + (2n + 1) \pi = 2 \pi \cdot 9.4 + (2n + 1) \pi$. Eine mögliche Lösung ist also $\varphi = 0.4 \pi$.
Woche 11 - Schrödingergleichung, Operatoren & Teilchen im Kasten
Theorie
Operatoren
In der Quantenmechanik benutzen wir häufig mathematische Objekte, die auf Funktionen wirken. Diese werden Operatoren genannt und werden mit einem Hut gekennzeichnet: $\hat{A}$. Ein Operator $\hat{A}$ wirkt auf eine Funktion $f(x)$ und liefert eine neue Funktion $\hat{A}f(x)$. Zum Beispiel ist die Ableitung ein Operator, der auf eine Funktion wirkt und als Ergebnis ('neue Funktion') ihre Ableitung liefert:
$$ \hat{\nabla}f(x) = \frac{\mathrm{d}}{\mathrm{d}x}f(x) = f'(x) $$
Ergibt die Anwendung eines Operators $\hat{A}$ auf eine Funktion $f$ wieder diese Funktion $f$ mal eine Konstante $\lambda$, so wird $f$ Eigenfunktion des Operators $\hat{A}$ zum Eigenwert $\lambda$ genannt. Wir schreiben:
$$ \hat{A}f(x) = \lambda f(x) \Leftrightarrow f \text{ ist Eigenfunktion von } \hat{A} $$
Born'sche Interpretation & Erwartungswerte
Die Wellenfunktion $\Psi(x)$ ist eine komplexe Funktion. Die Wahrscheinlichkeit, ein Teilchen an einem Ort $x$ zu finden, ist gleich dem Betragsquadrat der normierten Wellenfunktion:
$$ P(\vec{r}) = \left| \Psi(x) \right|^2 $$
und wird als Wahrscheinlichkeitsdichte bezeichnet. Damit die Wellenfunktion normiert ist, muss also gelten, dass die Wahrscheinlichkeit das Teilchen irgendwo im Raum zu finden gleich 1 ist:
$$ \int_{-\infty}^{\infty} \left| \Psi(x) \right|^2 \mathrm{d} x = 1 $$
Allgemeiner können wir jetzt auch den Erwartungswert eines Operators $\hat{A}$ berechnen:
$$ \langle \hat{A} \rangle = \int_{-\infty}^{\infty} \Psi^*(x) \hat{A} \Psi(x) \mathrm{d} x $$
Dabei ist $\Psi^*(x)$ die komplex konjugierte Wellenfunktion. Der Erwartungswert ist also der gewichtete Mittelwert des Operators $\hat{A}$ über alle möglichen Zustände $\Psi(x)$ und nimmt die Rolle der klassisch gemessenen Grösse ein.
Im Unterricht haben wir uns noch eine Veranschaulichung mit Mehl angeschaut:
Kommutatoren
Im Gegensatz zu den Zahlen, die wir in Alltagsrechungen verwenden, spielt es bei Operatoren eine Rolle in welcher Reihenfolge sie angewandt werden! Die Abhängigkeit der Reihenfolge wird durch den sogenannten Kommutator beschrieben:
$$ [\hat{A}, \hat{B}] = \hat{A}\hat{B} - \hat{B}\hat{A} $$
Wichtig beim Ausrechnen von Kommutatoren ist im Kopf zu behalten, dass Operatoren auf Funktionen wirken. Ich empfehle also immer $ [\hat{A}, \hat{B}]f(x) $ auszurechnen und nicht $ [\hat{A}, \hat{B}] $ alleine, da sonst schnell Fehler passieren. Ein Beispiel gibt es in den Aufgaben.
Schrödinger-Gleichung
In der Vorlesung habt ihr die Schrödinger-Gleichung kennengelernt. Diese lautet:
$$ \hat{H}\Psi(\vec{r},t) = \mathrm{i}\hbar\frac{\partial}{\partial t}\Psi(\vec{r},t) $$
Sie beschreibt also die zeitliche Entwicklung einer Wellenfunktion $\Psi(\vec{r}, t)$. Der darin vorkommende Operator $\hat{H}$ wird Hamilton-Operator genannt und ergibt sich durch die Quantisierung der klassischen Energie:
$$ \hat{H} = \frac{\hat{p}^2}{2m} + V(\vec{r}) $$
wobei $\hat{p} = -\mathrm{i}\hbar \hat{\nabla}$ der Impulsoperator und $V(\vec{r})$ das Potential repräsentiert.
Die Schrödinger-Gleichung scheint sich relativ einfach lösen zu lassen, vor allem wenn $\hat{H}$ nicht von der Zeit abhängt. Dann erhalten wir wie auch schon im Thema Radioaktivität gesehen eine Lösung der Form:
$$ \Psi(\vec{r}, t) = \Psi(\vec{r}, t=0) e^{- \mathrm{i} \hat{H} t/\hbar} $$
Die Anfangsfunktion $\Psi(\vec{r}, t=0)$ hängt nun nicht mehr von der Zeit ab und kann durch die Zeitunabhängige Schrödinger-Gleichung berechnet werden:
$$ \hat{H}\Psi(\vec{r}) = E\Psi(\vec{r}) $$
wobei $E$ die Energie des Systems im Zustand $\Psi(\vec{r})$ ist. Diese Gleichung ist eine Eigenwertgleichung, die Eigenfunktionen $\Psi(\vec{r})$ des Hamilton-Operators $\hat{H}$ zum Eigenwert $E$ beschreibt.
Aufgaben
Operatoren & Eigenfunktionen
- Zeige, dass die Funktion $f(x) = e^{kx}$ Eigenfunktion des Operators $\hat{A} = \dd{}{x}$ zum Eigenwert $k$ ist.
- Nenne zwei Eigenfunktionen des Operators $\hat{A} = \dd{}{x}$ zum Eigenwert $\lambda = 0$?
Kommutatoren
Berechne den Kommutator $ [\hat{A}, \hat{B}] $ von $\hat{A} = \hat{x}^2$ und $\hat{B} = \dd{}{x}$.
Schrödinger-Gleichung
Überprüfe, dass die vorhin gezeigte Funktion:
$$ \Psi(\vec{r}, t) = \Psi(\vec{r}) e^{- \mathrm{i} \hat{H} t/\hbar} $$
die Schrödinger-Gleichung erfüllt.
Erwartungswert
Angenommen wir betrachten ein Teilchen mit der Wellenfunktion $\Psi(x) = \begin{cases} A \sin(x), & \text{ für x} \in [0, \pi] \\ 0, & \text{sonst} \end{cases}$, wobei $A$ eine Normierungskonstante ist.
- Berechne die Normierungskonstante $A$. Hinweis: $\int sin^2(x) = \frac{x}{2} - \frac{\sin(x) \cos(x)}{2}$.
- Berechne die Wahrscheinlichkeit, das Teilchen im Intervall $[0, \pi/2]$ zu finden.
- Berechne den Erwartungswert des Ortsoperators $\hat{x}$, gegeben durch $\hat{x} = x$. Gib eine physikalische Interpretation an.
- Berechne den Erwartungswert des Impulsoperators $\hat{p}$, gegeben durch $\hat{p} = -\mathrm{i}\hbar \dede{}{x}$. Gib eine physikalische Interpretation an.
- Um was für eine Art von Potential könnte es sich handeln, in dem ein Teilchen mit so einer Wellenfunktion sich befindet?
Lösungen
Lösung Operatoren & Eigenfunktionen
- $$ \hat{A}f(x) = \dd{}{x} e^{kx} = k e^{kx} = kf(x) $$
- Irgendeine Konstante $c$ ist Eigenfunktion von $\dd{}{x}$ zum Eigenwert $\lambda = 0$, da $\hat{A}c = 0c = 0$.
Lösung Kommutatoren
Wie anfangs erklärt ist es wichtig, den Kommutator auf eine Funktion anzuwenden. Wir rechnen also:
$$ \begin{aligned} [x^2, \dd{}{x}] f(x) &= x^2 \dd{}{x} f(x) - \dd{}{x} \left( x^2 f(x) \right) \\ &= x^2 \dd{}{x} f(x) - \dd{}{x} x^2 f(x) \\ &= x^2 f'(x) - 2xf(x) - x^2 f'(x) \\ &= -2xf(x) \end{aligned} $$
Wobei wir die Produktregel für die Ableitung verwendet haben.
Lösung Schrödinger-Gleichung
Wir berechnen die Ableitung:
$$ \dede{}{t} \Psi(\vec{r}) e^{- \mathrm{i} \hat{H} t/\hbar} = - \frac{\mathrm{i}}{\hbar} \hat{H} \Psi(\vec{r}) e^{- \mathrm{i} \hat{H} t/\hbar} $$
und setzen dies in die Schrödinger-Gleichung ein:
$$ \begin{aligned} \hat{H} \Psi(\vec{r}, t) = \mathrm{i}\hbar\frac{\partial}{\partial t}\Psi(\vec{r},t) \\ \Leftrightarrow \hat{H} \Psi(\vec{r}) e^{- \mathrm{i} \hat{H} t/\hbar} = \mathrm{i} \hbar \cdot \left(-\frac{\mathrm{i}}{\hbar} \hat{H} \Psi(\vec{r}) e^{- \mathrm{i} \hat{H} t/\hbar} \right) \\ \Leftrightarrow \hat{H} \Psi(\vec{r}) e^{- \mathrm{i} \hat{H} t/\hbar} = \hat{H} \Psi(\vec{r}) e^{- \mathrm{i} \hat{H} t/\hbar} \end{aligned} $$
Die Schrödinger-Gleichung ist also erfüllt.
Lösung Erwartungswert
L1. Die Normierungskonstante $A$ ergibt sich aus der Normierungsbedingung
$$ \int_{-\infty}^{\infty} \left| \Psi(x) \right|^2 \mathrm{d} x = 1$$
Wir rechnen:
$$ \int_{-\infty}^{\infty} \left| \Psi(x) \right|^2 \mathrm{d} x = \int_{0}^{\pi} A^2 \sin^2(x) \mathrm{d} x = A^2 \frac{\pi}{2} $$
womit wir $A = \sqrt{\frac{2}{\pi}}$ erhalten.
L2. Die Wahrscheinlichkeit, das Teilchen im Intervall $[0, \pi/2]$ zu finden, ist $50\%$, da es sich gerade um die Hälfte des Intervalls $[0, \pi]$ handelt und die Wellenfunktion $\Psi(x)$ symmetrisch um $\pi/2$ ist. Wir können sie aber auch berechnen durch:
$$ \int_{0}^{\pi/2} \left| \Psi(x) \right|^2 \mathrm{d} x = \int_{0}^{\pi/2} \frac{2}{\pi} \sin^2(x) \mathrm{d} x = \frac{2}{\pi} \frac{\pi}{4} = \frac{1}{2} $$
L3. Der Erwartungswert des Ortsoperators $\hat{x}$ ist:
$$ \langle \hat{x} \rangle = \int_{-\infty}^{\infty} \Psi^*(x) \hat{x} \Psi(x) \mathrm{d} x = \int_{0}^{\pi} \frac{2}{\pi} \sin^2(x) x \mathrm{d} x = \frac{2}{\pi} \frac{\pi^2}{4} = \frac{\pi}{2} $$
Das Teilchen befindet sich also im Mittel bei $x = \pi/2$, was wir auch klassisch erwarten würden.
L4. Der Erwartungswert des Impulsoperators $\hat{p}$ ist:
$$ \begin{aligned} \langle \hat{p} \rangle &= \int_{-\infty}^{\infty} \Psi^*(x) \hat{p} \Psi(x) \mathrm{d} x = \int_{0}^{\pi} \frac{2}{\pi} \sin(x) \left(-\mathrm{i}\hbar \dede{}{x}\right) \sin(x) \mathrm{d} x \\ &= - \mathrm{i} \hbar \frac{2}{\pi} \int_{0}^{\pi} \sin(x) \cos(x) \mathrm{d} x = 0 \end{aligned}$$
Der Erwartungswert des Impulsoperators ist also $0$. Das Teilchen hat also im Mittel keinen Impuls, was wir auch klassisch erwarten würden, da es sich um eine stehende Welle handelt.
L5. Zuerst erkennen wir, dass das Teilchen sich nur in einer Dimension bewegen kann, da nur eine Ortsvariable $x$. Es handelt sich demnach auch um ein eindimensionales Potential. Da die Wellenfunktion ausserhalb des Bereiches $[0, \pi]$ verschwindet, muss das Potential ausserhalb dieses Bereiches unendlich gross sein, so dass die Aufenthaltswahrscheinlichkeit dort verschwindet. Innerhalb des Bereiches $[0, \pi]$ ist das Potential konstant, die Wellenfunktion eine Eigenfunktion von $\dede{^2}{x^2}$ und damit von $\hat p ^2$ ist. Es handelt sich also um ein Potential, das gerade dem in den Übungen betrachteten Potentials für das Teilchen im eindimensionalen Kasten entspricht.
Woche 12 - Wasserstoff-Atom & Atomterme
Theorie
Wasserstoff-Atom & Orbitale
Ihr habt in der Vorlesung gesehen, dass die (zeitunabhängige) Schrödingergleichung für das Wasserstoff-Atom analytisch lösbar ist. Die Lösungen davon sind 1-Elektronen-Wellenfunktionen und werden auch als Orbitale bezeichnet. Da wir die Schrödingergleichung für Atome mit mehreren Elektronen nicht analytisch lösen können, nähern wir diese oftmals mit den Lösungen des Wasserstoff-Atoms an. Diese Lösungen sind zwar nicht exakt, aber sie sind sehr gut und helfen uns, die Elektronenstruktur von Atomen zu verstehen.
Die Lösungen wurden separiert in ein Produkt von Radialteil, also vom Abstand zum Kern abhängigen, und Winkelteil, also von den Winkeln $\theta$ und $\phi$ abhängigen. Die genaue Form ist nicht weiter wichtig, die physikalische Interpretation der Knotenflächen hilft uns aber (v.a. in späteren Vorlesungen, AC, OC) die Reaktivität bestimmter Moleküle zu verstehen. Bei den Knotenflächen verschwindet die Wellenfunktion und somit auch ihr betragsquadrat. Nach der Born'schen Interpretation ist also die Aufenthaltswahrscheinlichkeit des Elektrons dort gleich 0!
Pauli-Aufbauprinzip
Da es sich bei Elektronen um Fermionen handelt, können zwei Elektronen nicht in allen der vier Quantenzahlen $n, l, m_l, m_s$ übereinstimmen. Weiter muss $l<n$ und $m_l \in {-l, -l+1, \dots, l-1, l},$ sowie $m_s \in {-\frac{1}{2}, \frac{1}{2}}$ gelten. Das auffüllen der Orbitale ist jedoch nicht ganz so einfach, als dass es einfach der Reihenfolge der Hauptquantenzahl $n$ nachgeht. Die Reihenfolge ist wie folgt dargestellt:
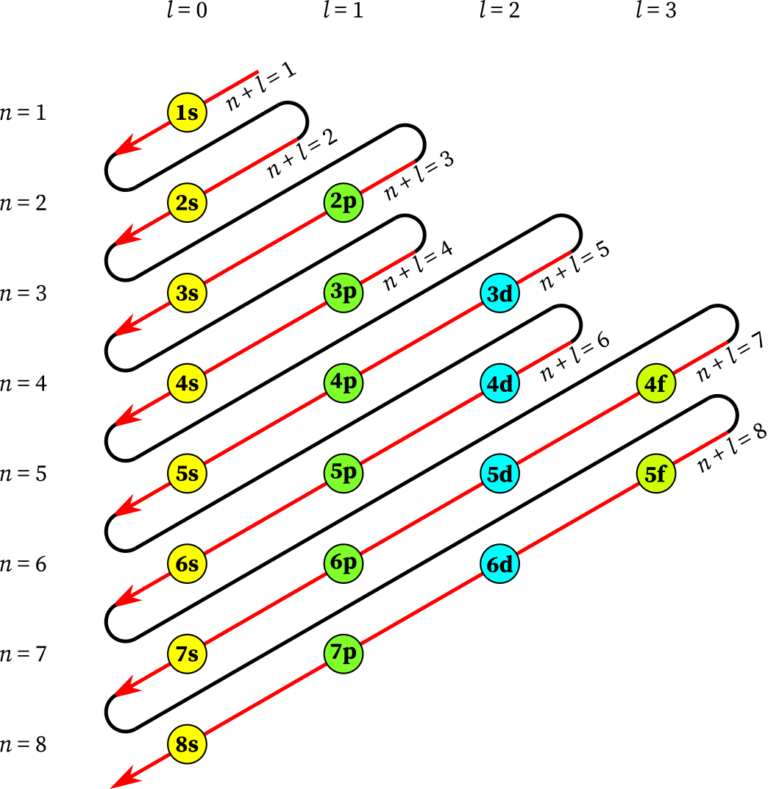
Die Orbitale mit der gleichen Quantenzahl $l$ werden auch als Unterschalen bezeichnet und können mit $2(l+1)$ Elektronen befüllt werden. Die Orbitale mit der gleichen Hauptquantenzahl $n$ werden auch als Schalen bezeichnet.
Termsymbole
Kochrezept zum bestimmen des Termsymbols:
- Orbitale besetzen nach dem Pauli-Prinzip (am besten aufzeichnen). Es müssen nur die Valenz-Elektronen betrachtet werden, da volle Unterschalen keinen Beitrag zum Gesamtdrehimpuls leisten.
- Bahndrehimpuls der einzelnen Elektronen $m_l$ zu Gesamtbahndrehimpuls $L$ addieren. Im Grundzustand werden die Orbitale so besetzt, dass $L$ maximal ist.
- Spindrehimpuls der einzelnen Elektronen $m_s$ zu Gesamtspindrehimpuls $S$ addieren. Im Grundzustand werden die Orbitale so besetzt, dass $S$ maximal ist.
- Gesamtbahndrehimpuls $L$ und Gesamtspindrehimpuls $S$ zu den möglichen Werten für den Gesamtdrehimpuls $J = L+S, L+S-1, \dots, |L-S|$ summieren. Im Grundzustand ist $$J = \begin{cases} L+S & \text{falls Unterschale mehr als halbvoll} \\ |L-S| & \text{falls Unterschale weniger als halbvoll} \end{cases}$$
- Das Termsymbol ist dann $^{2S+1}L_J$ (respektive mehrere, falls verschiedene Werte für $J$)
Beispiel für das Beryllium-Atom:
- 1s$^2$ 2s$^2$
- $m_{l,1} = 0, m_{l,2} = 0, m_{l,3} = 0, m_{l,4} = 0$ da alle in S-Orbitalen. Damit ist auch $L = 0$
- $m_{s,1} = +\frac{1}{2}, m_{s,2} = -\frac{1}{2}, m_{s,3} = +\frac{1}{2}, m_{s,4} = -\frac{1}{2}.$ Damit ist auch $S = 0$
- $J = 0 + 0 = 0$
- Das Termsymbol ist $^1\mathrm{S}_0$
Aufgaben
Termsymbole
Bestimme die Termsymbole für die folgenden Atome im Grundzustand:
a) Al
b) As
c) Welche der folgenden Termsymbole sind möglich und wieso/wieso nicht?
- $^3\mathrm{P}_2$
- $^0\mathrm{S}_0$
- $^7\mathrm{S}_3$
- $^1\mathrm{S}_1$
Grundlagen und Modelle der QM (Prüfung HS10)
In einem ersten Experiment misst du den Impuls eines Elektrons in $x$-Richtung und dann den Impuls in $z$-Richtung. In einem zweiten Experiment führst du diese Messungen genau in umgekehrter Reihenfolge durch.
a) Formuliere diese beiden Messungen in der Sprache der QM (mit Operatoren).
b) Gib an, was die Differenz der Messergebnisse ist und begründe deine Antwort mathematisch!
Ein Proton befindet sich in einem eindimensionalen Kasten der Länge $d = 1.5\, \mathrm{fm}$.
c) Berechne die Wellenlänge der elektromagnetischen Strahlung, die emittiert wird, wenn das Proton einen Übergang von $n = 2$ nach $n = 1$ erfährt.
d) In welchem Bereich des elektromagnetischen Spektrums liegt die emittierte Strahlung?
Berechne unter der Annahme einer quantenmechanischen harmonischen Oszillation die minimale Anregungsenergie vom Grundzustand in den ersten angeregten Zustand für
e) einen Schwingquarz einer Uhr bei $33 \, \mathrm{kHz}$;
f) die Bindung zwischen zwei Sauerstoffatomen im Sauerstoffmolekül. Die Kraftkonstante betrage $k = 1177 \, \mathrm{N/m}$.
Tipp: Als Masse ist die reduzierte Masse für zwei Teilchen $1$ und $2$: $\mu = \frac{m_1 m_2}{m_1 + m_2}$ zu verwenden und die Masse eines Sauerstoffatoms sei aus der molaren Masse zu berechnen.
Lösungen
Lösung Termsymbole
a) Al: $[\mathrm{Ne}] 3s^2 3p^1 \Rightarrow L = 1, S = \frac{1}{2} \Rightarrow ^2P_{\frac{1}{2}}$
b) As: $[\mathrm{Ar}] 3d^{10} 4s^2 4p^3 \Rightarrow L = 0, S = 3/2 \Rightarrow ^4S_{\frac{3}{2}}$
c) Erinnere dich daran, dass das Termsymbol $^{2S+1}L_J$ ist, wobei $S$ der Gesamtspindrehimpuls, $L$ der Gesamtbahndrehimpuls und $J$ der Gesamtdrehimpuls ist. Die möglichen Werte für $J$ sind $J = L+S, L+S-1, \dots, |L-S|$. Damit gilt:
- möglich, z.B. für Grundzustand von Schwefel
- nicht möglich, da $2S+1 \geq 1$ sein muss.
- möglich, z.B. für Grundzustand von Chrom
- nicht möglich, da $\mathrm{S} \Leftrightarrow L = 0$ und $2S+1 = 1 \Rightarrow S = 0,$ jedoch $J = 1,$ was zu einem Widerspruch führt.
Lösung Grundlagen und Modelle der QM (Prüfung HS10)
a) Die Operatoren von der Sicht der Wellenfunktion $\psi_{el}$ aus in der gegebenen Reihenfolge aufgeschrieben werden, da sie in dieser Reihenfolge angewendet werden (also gerade umgekehrt die wir es aufschreiben würden):
- Messung (zuerst Impuls in $x$-Richtung, dann Impuls in $z$-Richtung) $ M_1: \hat{p}_z \hat{p}_x \psi_{el} $
- Messung (zuerst Impuls in $z$-Richtung, dann Impuls in $x$-Richtung) $ M_2: \hat{p}_x \hat{p}_z \psi_{el} $
b) Die Differenz erhalten wir aus dem Kommutator der beiden Operatoren $\hat{p}_z$ und $\hat{p}_x$. Da diese kommutieren, ist der Kommutator gleich Null. Es gibt also keine Differenz zwischen den beiden Messergebnissen.
c) Die Energielevels des Teilchen im Kasten sind bekannt:
$$E_n = \frac{n^2 h^2}{8 m_p d^2} \Rightarrow E_{2 \rightarrow 1} = 3 \frac{h^2}{8 m_p d^2}$$
$$\lambda = \frac{hc}{E_{2 \rightarrow 1}} \approx 4.54 \cdot 10^{-15} \, \mathrm{m}$$
d) Die emittierte Strahlung ist sehr kurzwellig und liegt im Bereich der $\gamma$-Strahlung.
e) Mit der Lösung des harmonischen Oszillator:
$$E_n = \left(n + \frac{1}{2}\right) h \nu$$
erhalten wir direkt:
$$E_{0 \rightarrow 1} = h \nu \approx 2.19 \cdot 10^{-29} \, \mathrm{J}$$
f) Da die Bindung als harmonischer Oszillator modelliert werden kann, gilt die gleiche Formel wie in e). Die Frequenz erhalten wir aus der Kraftkonstante $k$:
$$\nu = \frac{1}{2 \pi} \sqrt{\frac{k}{\mu}}$$
Die reduzierte Masse zwischen zwei Sauerstoffatomen der Masse $m_{O} \approx 16 \, \mathrm{u}$ ist:
$$\mu = \frac{m_{O}^2}{2 m_{O}} = \frac{m_{O}}{2}$$
Es ergibt sich:
$$E_{0 \rightarrow 1} = h \nu = h \frac{1}{2 \pi} \sqrt{\frac{k}{\mu}} = \frac{h}{2 \pi} \sqrt{\frac{2 k}{m_{O}}} \approx 3.14 \cdot 10^{-20} \, \mathrm{J}$$
Woche 13 - Harmonischer Oszillator
Theorie
Harmonischer Oszillator
Definition
Ein harmonischer Oszillator ist ein System, das durch die folgende Differentialgleichung beschrieben wird:
$$\frac{\mathrm d^2 f(x)}{\mathrm d x^2} = - \omega^2 f(x)$$
wobei $\omega$ eine Konstante ist. Die Lösung dieser Differentialgleichung ist:
$$f(x) = A \sin(\omega x) + B \cos(\omega x)$$
und beschreibt eine harmonische Schwingung mit der Kreisfrequenz $\omega$.
Diese Differentialgleichung erhalten wir, wenn ein Kraftgesetz der Form $F(x) = - k (x - x_{\mathrm e})$ gilt, also die Kraft proportional zur Auslenkung aus einer Gleichgewichtsposition $x_{\mathrm e}$ ist. Die Konstante $k$ ist die Kraftkonstante und $\omega = \sqrt{\frac{k}{m}}$ ist die oben bereits vorgekommene Kreisfrequenz. Das zugehörige Potential ist dann $V(x) = \frac{1}{2} k (x - x_{\mathrm e})^2 ,$ was wir meist antreffen werden.
Motivation
Da die Natur nach dem Zustand der niedrigsten Energie strebt, ist es naheliegend, dass sich ein Teilchen in einem Potential zumindest an einem lokalen Minimum befindet wird. Der harmonische Oszillator ist ein wichtiges Modell in der Physik, da kleine Auslenkungen aus einem Gleichgewichtszustand durch ein harmonisches Potential approximiert werden können. Betrachten wir nun eine kleine Störung vom Gleichgewichtszustand und nähern wir das Potential durch eine Taylor-Entwicklung zweiter Ordnung an, so erhalten wir ein harmonisches Potential:
$$V(x) \approx V(x_{\mathrm e}) + \frac{1}{2} V''(x_{\mathrm e}) (x-x_{\mathrm e})^2$$
Da wir den Nullpunkt des Potentials frei wählen können, können wir $V(x_{\mathrm e}) = 0$ setzen und erhalten:
$$V(x) \approx \frac{1}{2} V''(x_{\mathrm e}) (x-x_{\mathrm e})^2$$
Harmonischer Oszillator in der Quantenmechanik
Betrachten wir den harmonischen Oszillator in der Quantenmechanik, so benötigen wir die zeitunabhängige Schrödinger-Gleichung:
$$\left( - \frac{\hbar^2}{2 m} \frac{\mathrm d^2}{\mathrm d x^2} + \frac{1}{2} k x^2 \right) \psi(x) = E \psi(x)$$
Die Lösungen dieser Differentialgleichung sind schön kompliziert und interessieren uns nicht direkt. Wichtig sind die Eigenwerte, die wir für die Energie erhalten:
$$E_n = \hbar \omega \left( n + \frac{1}{2} \right) = h \nu \left( n + \frac{1}{2} \right)$$
wobei $n$ eine natürliche Zahl und $\nu = \frac{1}{2 \pi} \sqrt{\frac{k}{m}}$ die Frequenz der harmonischen Schwingung ist. Im harmonischen Potential können also nur bestimmte Frequenzen angenommen werden, was auch experimentell in der Infrarot-Spektroskopie beobachtet werden kann.
Aufgaben
Verständnisfragen Harmonischer Oszillator
a) Eine Taylor-Entwicklung zweiter Ordnung hat die Form:
$$f(x) \approx f(x_0) + f'(x_0) (x-x_0) + \frac{1}{2} f''(x_0) (x-x_0)^2$$
Im Theorie-Teil haben wir aber gesagt, dass die Taylor-Entwicklung zweiter Ordnung von $V(x)$ die Form
$$V(x) \approx V(x_{\mathrm e}) + \frac{1}{2} V''(x_{\mathrm e}) (x-x_{\mathrm e})^2$$
hat. Was ist mit dem Term $V'(x_{\mathrm e}) (x-x_{\mathrm e})$ passiert?
b) Was ist der Unterschied zwischen dem harmonischen Oszillator in der klassischen Mechanik und in der Quantenmechanik?
c) Funktioniert die Approximation der Wasserstoff-Bindung durch ein harmonisches Potential besser für kleine oder für grosse Auslenkungen? Begründe deine Antwort.
d) Könnte die Wasserstoff-Bindung wirklich durch ein harmonisches Potential beschrieben werden, könnte sie dann dissoziieren? Begründe deine Antwort.
Dissoziation von Wasserstoff (Prüfung FS17)
Wasserstoffmoleküle werden aus einer Mischung von H-, D- und T-Atomen mit relativer Häufigkeit von $60 \%$, $30 \%$ und $10 \%$ gebildet. Dabei werden alle Atome verbraucht, und es entstehen nicht nur $\mathrm{H}_2$-Moleküle, sondern auch D- und T-haltige Isotopomere von $\mathrm{H}_2$.
a) Liste alle Wasserstoffisotopomere auf, die aus der Mischung gebildet werden können und gib jeweils deren relativen Häufigkeiten an.
Die Dissoziationsenergie $D_0$ von $\mathrm{H}_2$ beträgt $7.17466 \cdot 10^{-19} \, \mathrm{J}.$ Die harmonische Schwingungsfrequenz von $\mathrm{H}_2$ beträgt $\mu = 1.3176 \cdot 10^{14} \, \mathrm{Hz},$ und der Gleichgewichtsabstand von $\mathrm{H}_2$ ist $R_e = 0.739 \cdot 10^{-10} \, \mathrm{m}.$
b) Skizziere in einem Diagramm den Verlauf der Born-Oppenheimer-Potentialenergie $V(R)$ von $\mathrm{H}_2$ als Funktion des internuklearen Abstands $R$ zwischen den zwei Protonen. Markiere in diesem Diagramm die Dissoziationsenergien $D_0$ und $D_e$.
c) Bestimme den Wert von $D_e$ möglichst genau.
d) Bestimme die harmonische Schwingungswellenzahl von $\mathrm{H}_2$ und $\mathrm{HD}$ und schätze die Dissoziationsenergie $D_0$ von $\mathrm{HD}$ mit den obigen Angaben möglichst genau ab.
e) Welches der unter a) ermittelten Isotopomeren hat die höchste Dissoziationsenergie $D_0 \mathrm{?}$
Lösungen
Lösung Verständnisfragen Harmonischer Oszillator
a) Da $V(x)$ bei $x_{\mathrm e}$ ein lokales Minimum hat, muss $V'(x_{\mathrm e}) = 0$ gelten. Somit fällt der Term $V'(x_{\mathrm e}) (x-x_{\mathrm e})$ weg.
b) Beim harmonischen Oszillator in der klassischen Mechanik ist die Energie kontinuierlich, während sie in der Quantenmechanik diskret ist, also nur bestimmte Werte annehmen kann.
c) Die Approximation funktioniert besser für kleine Auslenkungen, da die Terme höherer Ordnung in der Taylor-Entwicklung dann vernachlässigt werden können. Wenn $x^2$ klein ist, dann ist $x^3$ noch kleiner und $x^4$ noch kleiner, etc.
d) Sie könnte nicht dissoziieren, da die wirkende Kraft proportional zur Auslenkung ist. Wenn die Auslenkung gross wird, wird die Kraft gross und zieht das Molekül wieder zurück. Es wird nie ein Zustand erreicht, bei dem die Kraft zwischen den Atomen verschwindet und das Molekül somit dissoziierte.
Lösung Dissoziation von Wasserstoff (Prüfung FS17)
a) Es können die Isotopomere $\mathrm{H}_2$, $\mathrm{HD}$, $\mathrm{HT}$, $\mathrm{D}_2$, $\mathrm{DT}$ und $\mathrm{T}_2$ gebildet werden. Die relativen Häufigkeiten sind:
| Isotopomer | Häufigkeit |
|---|---|
| $\mathrm{H}_2$ | $0.6^2 = 0.36$ |
| $\mathrm{HD}$ | $2 \cdot 0.6 \cdot 0.3 = 0.36$ |
| $\mathrm{HT}$ | $2 \cdot 0.6 \cdot 0.1 = 0.12$ |
| $\mathrm{D}_2$ | $0.3^2 = 0.09$ |
| $\mathrm{DT}$ | $2 \cdot 0.3 \cdot 0.1 = 0.06$ |
| $\mathrm{T}_2$ | $0.1^2 = 0.01$ |
Zur Überprüfung, die Summe der Häufigkeiten ist: $0.36 + 0.36 + 0.12 + 0.09 + 0.06 + 0.01 = 1$.
b)
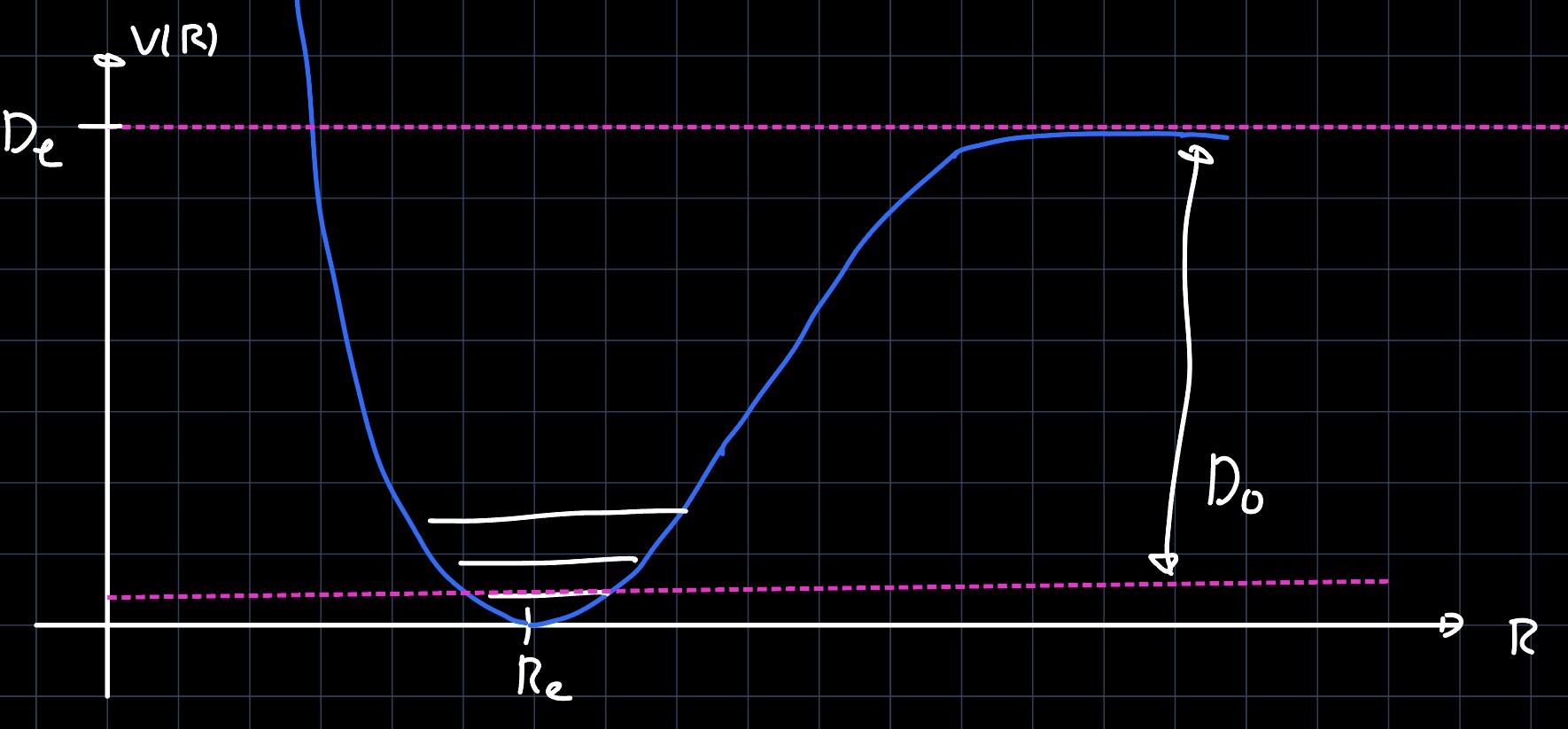
c) $D_e \approx D_0 + \frac{1}{2} h \nu \approx 7.6112 \cdot 10^{-19} \, \mathrm{J}$
d) Die harmonische Schwingungswellenzahl für $\mathrm{H}_2$ erhalten wir aus der Schwingungsfrequenz $\nu \approx 1.3176 \cdot 10^{14} \, \mathrm{Hz}$:
$$\tilde{\nu}_{\mathrm{H}_2} = \frac{\nu}{c} \approx 4395\, \mathrm{cm}^{-1}$$
Die harmonische Schwingungswellenzahl für $\mathrm{HD}$ erhalten wir über die Formel $\nu = \frac{1}{2 \pi} \sqrt{\frac{k}{\mu}}$ und der Annahme, dass die Kraftkonstante $k$ gleich bleibt:
$$\tilde{\nu}_{\mathrm{HD}} = \sqrt{\frac{m_n + 2 m_p}{2(m_n+m_p)}} \tilde{\nu}_{\mathrm{H}_2} \approx 3108\, \mathrm{cm}^{-1}$$
Somit erhalten wir für die Dissoziationsenergie von $\mathrm{HD}$:
$$D_{0, \mathrm{HD}} \approx D_{e, \mathrm{H}_2} - \frac{1}{2} h c \tilde{\nu}_{\mathrm{HD}} \approx 7.3025 \cdot 10^{-19} \, \mathrm{J}$$
e) $D_0$ wird maximal, wenn $\tilde{\nu}$ minimal ist. Dies ist der Fall, wenn $\frac{{\mu}_{\mathrm{H}_2}}{{\mu}_\mathrm{XY}}$ minimal ist. Setzen wir $m_X, m_Y$ ein, so erhalten wir:
$$\frac{\frac{m_p}{2}}{\frac{m_X m_Y}{m_X + m_Y}} = \frac{m_p}{2} \frac{m_X + m_Y}{m_X m_Y}$$
was gerade minimal wird, wenn $m_X = m_Y = m_p$ ist. Somit ist $\mathrm{H}_2$ das Isotopomer mit der höchsten Dissoziationsenergie.
Woche 14 - Prüfungsvorbereitung
Prüfungsrelevantes
Ich habe in der PPP der Vorlesung markiert, welche Teile ich für Prüfungsrelevant halte und was ihr einfach mal gesehen haben solltet, aber nicht erwartet wird, dass ihr es wiedergeben könnt. Dieses Dokument ist hier verfügbar. Angaben ohne Gewähr
Prüfungsvorbereitung
Allgemein - Organisatorisch
Da ihr die Basisprüfung als Block schreibt, habt ihr erst im Sommer Prüfungen. Das heisst aber nicht, dass ihr im Winter nicht schon mit der Vorbereitung anfangen solltet! Ich empfehle, in der vorlesungsfreien Zeit den gelernten Stoff zu repetieren und ggfs. Zusammenfassungen zu schreiben. Ausserdem würde ich die Übungen nochmals durchgehen, da diese auch zum Prüfungsstoff gehören.
Irgendwann Mitte Frühlingssemester kommt die Ankündigung, dass ihr euch für die Prüfungen anmelden kommt per Mail. Mit ein Paar Klicks im myStudies seid ihr angemeldet und müsst euch um nichts mehr kümmern. Die genauen Prüfungsdaten werden ca. 2 Monate danach bekannt gegeben.
Nach dem Frühlingssemester beginnt die Lernphase. Diese ist sehr lang, also empfiehlt es sich nicht gleich die ganze Energie am Anfang zu verpuffen und vielleicht erst mal 1-2 Wochen Ferien zu machen. Wenn ihr müde und überlastet seid, bringt das Lernen mässig viel. Danach ist es wichtig einen Lernplan anzufertigen, um den Überblick über die vielen Fächer zu behalten. Die ETH stellt euch dafür und auch allgemein für die Prüfungsvorbereitung Beratung und Hilfsmittel zur Verfügung. Auch hier: Nehmt es ernst euch nicht zu überlasten und gönnt euch Wochenenden und Pausen!
ACPC I Prüfung - Organisatorisch
- Die Prüfung dauert 60 Minuten und es gibt (normalerweise) 3 Aufgaben ca. von der Länge einer Übungsaufgabe. Es gibt also recht zeitdruck.
- PC0 wird zusammen mit PCI - Thermodynamik geprüft. Ihr schreibt zuerst die PC0 Prüfung, dann gibt es ein paar Minuten Pause bevor die PCI Prüfung dran kommt.
- Die Prüfung ist open-book. Ihr dürft also alle schriftlichen Unterlagen mitnehmen, sowie einen beliebigen (nicht Internetfähigen) Taschenrechner.
- Normalerweise ist eine Aufgabe zu Radioaktivität, eine zu QM und die dritte variiert (z.B. zum (an)harmonischen Oszillator, zu Atomtermen, etc.)
ACPC I Spezifische Tipps - Lernen
- Es gibt viele Altprüfungen in der Prüfungssammlung vom VCS. Diese sind sehr hilfreich um zu üben. Die Prüfungen sind meist sehr ähnlich aufgebaut.
- Beim Altprüfungen lösen ist es wichtig, diese auch zu korrigieren. Seid streng mit euch und löst die Aufgaben, die ihr falsch gemacht habt nochmal mit 'spicken' in der Musterlösung.
- Lernt nicht nur mit Altprüfungen, sondern schaut auch die Theorie nochmals an. Die Prüfung kann auch plötzlich etwas anders aussehen.
ACPC I Spezifische Tipps - Prüfung
- Wie bereits mehrfach betont: Besorgt euch einen guten Taschenrechner und benutzt auch dessen Vorteile! Vergesst nicht dafür Youtube-Video von Raphael anzusehen.
- Eine Stunde reicht kaum um die ganze Prüfung zu lösen. Ihr müsst also Prioritäten setzen und zuerst die Aufgaben lösen, die ihr am besten könnt. Dabei lohnt es sich meist die letzten paar Teilaufgaben einer Aufgabe wegzulassen: Diese sind oft schwieriger und bringen nur wenige Punkte.
- Macht euch keine Sorgen beim lernen, wenn ihr die Prüfungen nicht in der gegebenen Zeit lösen könnt. Meist habt ihr ab ca. $40\%$ der Punkte bestanden und mit $2/3$ der Punkte die $6$.

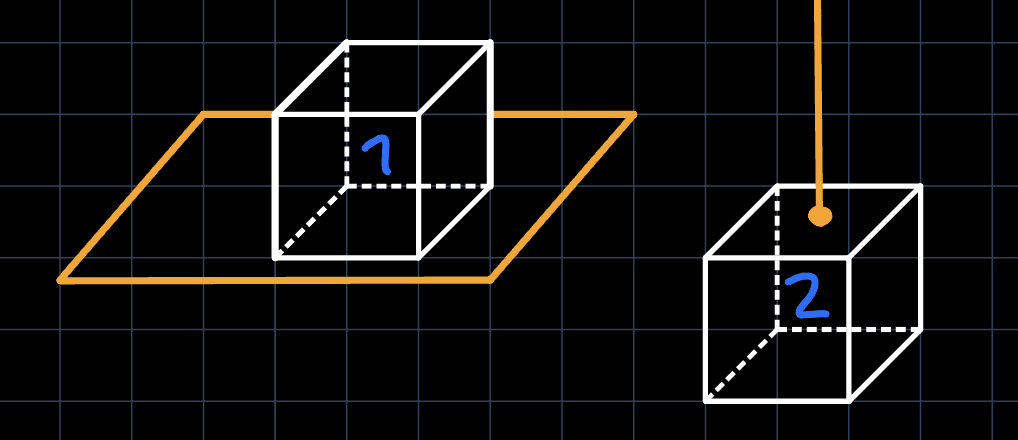

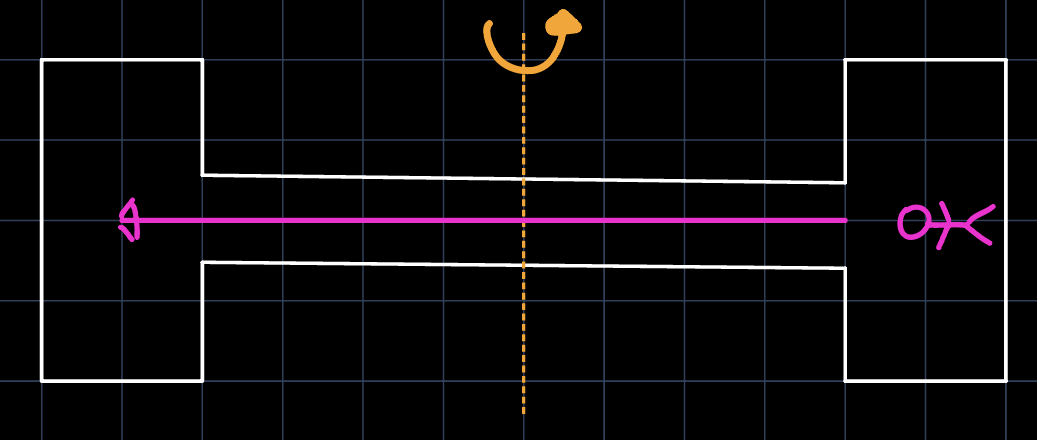
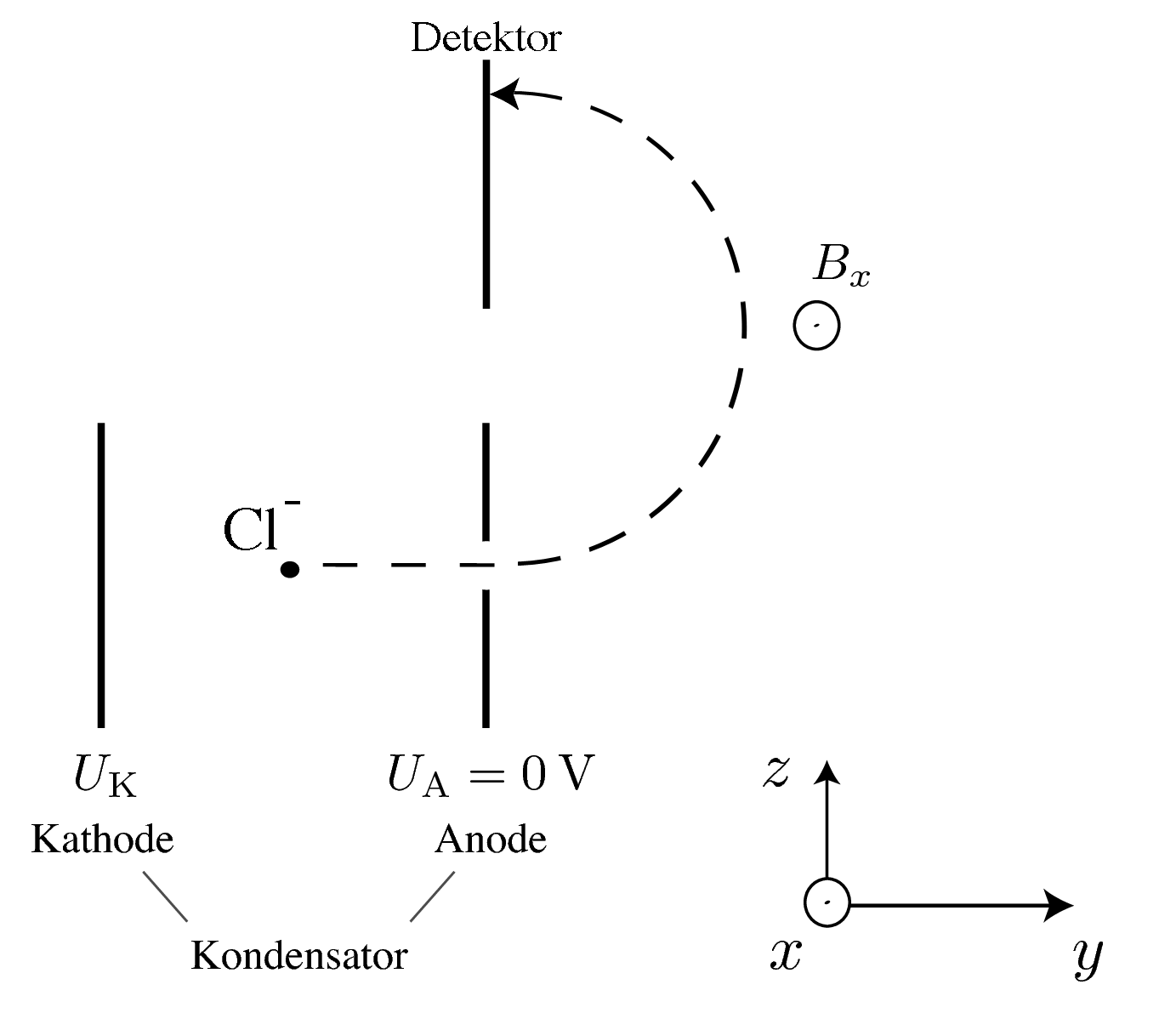
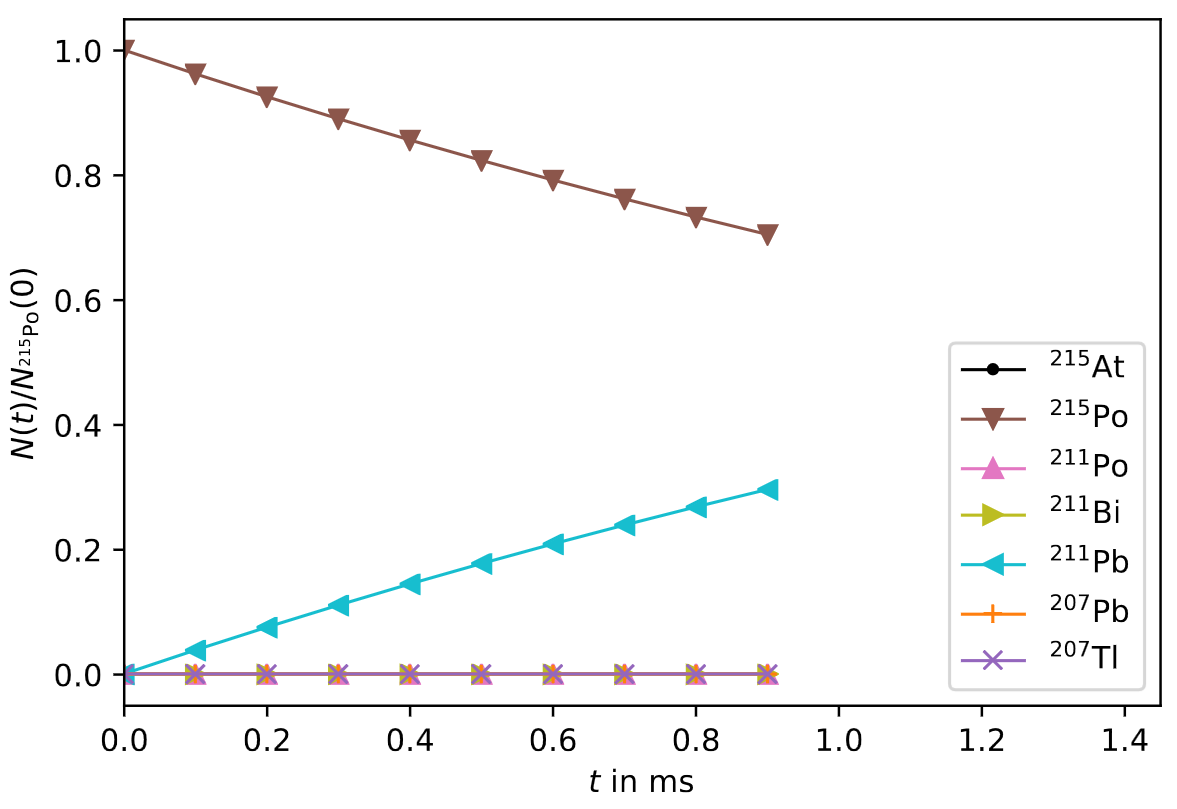
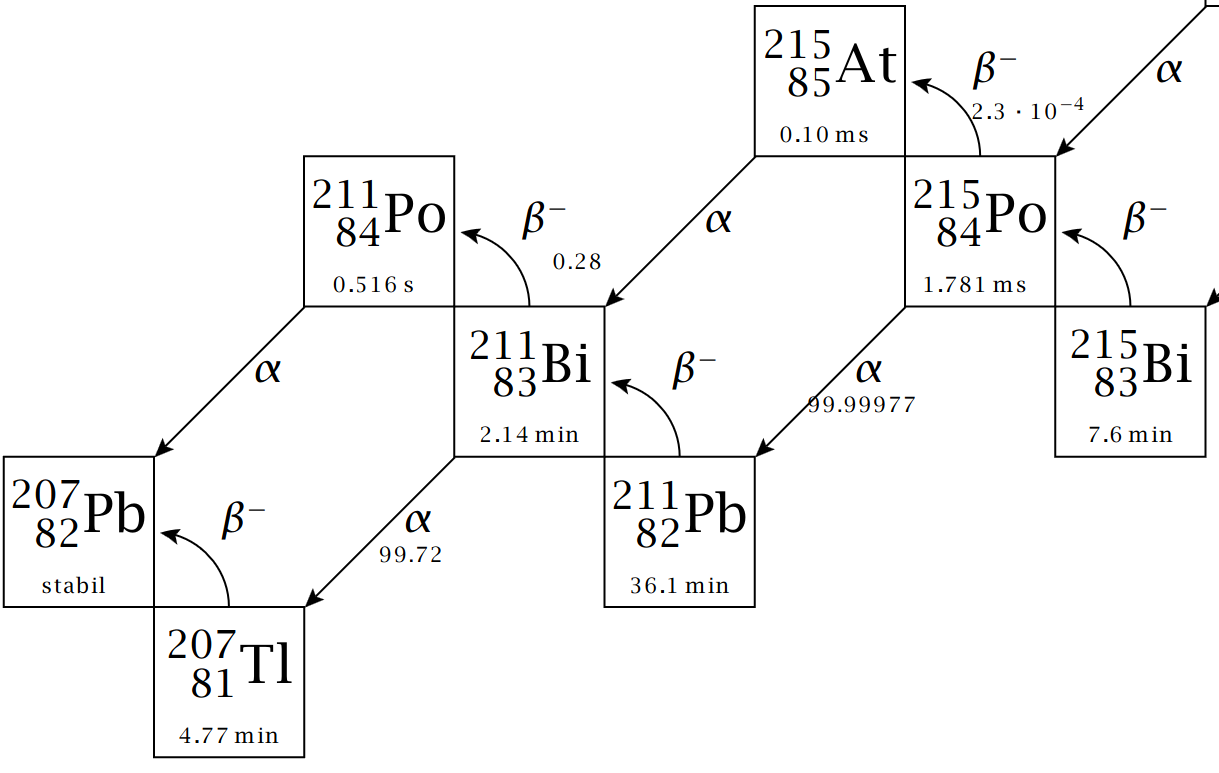
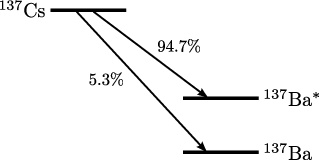
 Die minimale Energie, um ein Elektron aus einer Metalloberfläche freizusetzen, ist die Austrittsarbeit $E_{\rm Aus}$ und stellt die Bindungsenergie des Elektrons im Metall dar. Bei der Bestrahlung einer metallischen Oberfläche mit monochromatischen Licht werden Elektronen emittiert, wenn die absorbierte Energie die Austrittsarbeit überschreitet. Die Austrittsarbeit der meisten Metalle liegt im ultravioletten bis sichtbaren Bereich des elektromagnetischen Spektrums.
Die minimale Energie, um ein Elektron aus einer Metalloberfläche freizusetzen, ist die Austrittsarbeit $E_{\rm Aus}$ und stellt die Bindungsenergie des Elektrons im Metall dar. Bei der Bestrahlung einer metallischen Oberfläche mit monochromatischen Licht werden Elektronen emittiert, wenn die absorbierte Energie die Austrittsarbeit überschreitet. Die Austrittsarbeit der meisten Metalle liegt im ultravioletten bis sichtbaren Bereich des elektromagnetischen Spektrums.